No CrossRef data available.
Article contents
Two interpolation theorems for a 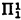 predicate calculus1
predicate calculus1
Published online by Cambridge University Press: 12 March 2014
Extract
A second order formula is called Π1 if, in its prenex normal form, all second order quantifiers are universal. A sequent F1, … Fm → G1 …, Gn is called Π1 if a formula
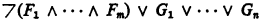
is Π1
If we consider only Π1 sequents, then we can easily generalize the completeness theorem for the cut-free first order predicate calculus to a cut-free Π1 predicate calculus.
In this paper, we shall prove two interpolation theorems on the Π1 sequent, and show that Chang's theorem in [2] is a corollary of our theorem. This further supports our belief that any form of the interpolation theorem is a corollary of a cut-elimination theorem. We shall also show how to generalize our results for an infinitary language. Our method is proof-theoretic and an extension of a method introduced in Maehara [5]. The latter has been used frequently to prove the several forms of the interpolation theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1971
Footnotes
Part of this work was supported by NSF GP 14134.

