Article contents
Two remarks on the Lifschitz realizability topos
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this note is to clarify two points about the topos Lif, introduced in [13] as a generalization of Lifschitz' realizability ([9, 12]). Lif is a subtopos of Hyland's Effective topos 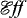 ([1]). The points I want to make are:
([1]). The points I want to make are:
Remark 1. Lif is the largest subtopos of 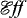 satisfying the axiom (O):
satisfying the axiom (O):
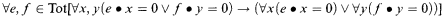
where  denotes partial recursive application, and “∈ Tot” means that e and f range over codes for total recursive functions. One may read (O) as the statement “The union of two
denotes partial recursive application, and “∈ Tot” means that e and f range over codes for total recursive functions. One may read (O) as the statement “The union of two 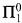 -sets is again a
-sets is again a 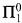 -set”. That is, let
-set”. That is, let 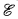 be a subtopos of
be a subtopos of 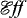 . Then (O) is true in
. Then (O) is true in 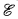 for the standard interpretation (the variables range over the natural numbers object of
for the standard interpretation (the variables range over the natural numbers object of 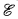 , etc.) if and only if the inclusion
, etc.) if and only if the inclusion 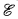 ↣
↣ 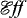 factors through the inclusion Lif ↣
factors through the inclusion Lif ↣ 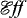 .
.
Remark 2. Like 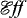 , Lif contains at least two weakly complete internal full subcategories, thus providing us with more models of polymorphism and other impredicative type theories.
, Lif contains at least two weakly complete internal full subcategories, thus providing us with more models of polymorphism and other impredicative type theories.
The principle (O) has some standing in the history of constructive mathematics:
- H. Friedman has proved that (O) is equivalent to a formulation of intuitionistic completeness of the intuitionistic predicate calculus for Tarskian semantics; see [8]. This is not to imply that this result is of immediate relevance to Lif: Friedman works in a system of analysis, a theory of lawless sequences with an axiom of “open data” for arithmetical formulas, which at least for the domain of all functions from N to N fails in Lif. However, there might exist a “nonstandard model” of arithmetic and a corresponding system of analysis, in which we may be able to carry out his proof.
- Moreover, Remark 2 entails that Lif should provide us with models of synthetic domain theory (for an exposition, see [3]), and one with the nice property that the dual of one of the axioms (axiom 7 in [3]) comes for free, by (O).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 2
- Cited by

