UFA fails in the Bell-Kunen model

Extract

In [vDF], van Douwen and Fleissner introduce a number of axioms which hold in models constructed by iteratively forcing MA in a nontrivial extension of the set-theoretic universe. One such model is the Bell-Kunen model, obtained by starting with a model of ZFC + GCH, then forcing “MA + ϲ = ω₂” by the standard means, then forcing “MA + ϲ = ω₃”, and so on. The Bell-Kunen model is the result of an ω₁ sequence of extensions of this form, with direct limits taken at limit ordinals. (See [BK] for a more complete description.) Van Douwen and Fleissner observed that many of the properties of this model could be distilled into a “Definable Forcing Axiom”, which states that “If P is a c.c.c. partial order which is definable from a real, then there is a sequence of filters through 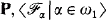, such that if 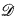is any dense subset of P, then all but countably many of the ℱ_α's meet in a nonempty set.” (They call such a sequence ω₁-generic.) Van Douwen and Fleissner ask whether one can eliminate the restriction on the c.c.c. order entirely; the resulting axiom (“If P is any c.c.c. partial order of cardinality at most ϲ, then there is a sequence of filters…”) is called the Undefinable Forcing Axiom (UFA).