U-meager sets when the cofinality and the coinitiality of U are uncountable

Abtract

We prove that every countably determined set C is U-meager if and only if every internal subset A of C is U-meager, provided that the cofinality and coinitiality of the cut U are both uncountable. As a consequence we prove that for such cuts a countably determined set C which intersects every U-monad in at most countably many points is U-meager. That complements a similar result in [KL]. We also give some partial solutions to some open problems from [KL]. We prove that the set 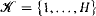, where H is an infinite integer, cannot be expressed as a countable union of countably determined sets each of which is U-meager for some cut U with min{cf(U), ci(U)} ≥ ω₁. Also, every Borel, 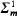or countably determined set C which is U-meager for every cut U is a countable union of Borel, 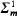or countably determined sets respectively, which are U-nowhere dense for every cut U. Further, the class of Borel U-meager sets for min{cf(U),ci(U)} ≥ ω₁ coincides with the least family of sets containing internal U-meager sets and closed with respect to the operation of countable union and intersection. The same is true if the phrase “U-meager sets” is replaced by “U-meager for every cut U.”