Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shelah, Saharon
and
Väisänen, Pauli
2002.
Almost free groups and Ehrenfeucht–Fraı̈ssé games for successors of singular cardinals.
Annals of Pure and Applied Logic,
Vol. 118,
Issue. 1-2,
p.
147.
Väisänen, Pauli
2003.
Almost free groups and long Ehrenfeucht–Fraı̈ssé games.
Annals of Pure and Applied Logic,
Vol. 123,
Issue. 1-3,
p.
101.
Väänänen, Jouko
2008.
The Craig Interpolation Theorem in abstract model theory.
Synthese,
Vol. 164,
Issue. 3,
p.
401.

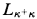 under the assumption
under the assumption 