Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T02:04:19.181Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVERSAL SUBGROUPS OF POLISH GROUPS

Published online by Cambridge University Press:  12 December 2014

KONSTANTINOS A. BEROS
KONSTANTINOS A. BEROS*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NORTH TEXAS GENERAL ACADEMICS BUILDING 435 1155 UNION CIRCLE DENTON, TX 76203-5017, USA E-mail:beros@unt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a class 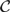${\cal C}$ of subgroups of a topological group G, we say that a subgroup 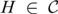$H \in {\cal C}$ is a universal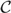${\cal C}$subgroup of G if every subgroup 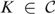$K \in {\cal C}$ is a continuous homomorphic preimage of H. Such subgroups may be regarded as complete members of 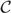${\cal C}$ with respect to a natural preorder on the set of subgroups of G. We show that for any locally compact Polish group G, the countable power Gω has a universal Kσ subgroup and a universal compactly generated subgroup. We prove a weaker version of this in the nonlocally compact case and provide an example showing that this result cannot readily be improved. Additionally, we show that many standard Banach spaces (viewed as additive topological groups) have universal Kσ and compactly generated subgroups. As an aside, we explore the relationship between the classes of Kσ and compactly generated subgroups and give conditions under which the two coincide.

Keywords

03E1554H1122A0520B3020B35
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 4 , December 2014 , pp. 1148 - 1183
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Becker, Howard and Kechris, Alexander S., The descriptive set theory of polish group actions, London Mathematical Society Lecture Note Series, vol. 232, Cambridge University Press, Cambridge, 1996.Google Scholar
Beros, Konstantinos A., Universal subgroups at each projective level, 2013, preprint, http://arxiv.org/abs/1306.4940.Google Scholar
Blass, Andreas, The Rudin-Keisler ordering of P-points. Transactions of the American Mathematical Society, vol. 179 (1973), pp. 145–166.Google Scholar
Booth, David, Ultrafilters on a countable set. Annals of Mathematical Logic, vol. 2 (1970/1971), no. 1, pp. 1–24.CrossRefGoogle Scholar
Conway, John B., A course in functional analysis, Graduate Texts in Mathematics, second ed.,vol. 96, Springer-Verlag, 1990.Google Scholar
Enflo, Per, A counterexample to the approximation problem in Banach spaces. Acta Mathematica, vol. 130 (1973), pp. 309–317.CrossRefGoogle Scholar
Ferenczi, Valentin, Operators on subspaces of hereditarily indecomposable Banach spaces. Bulletin of the London Mathematical Society, vol. 29 (1997), no. 3, pp. 338–344.CrossRefGoogle Scholar
Gao, Su, Invariant descriptive set theory, Taylor & Francis Group, 2009.Google Scholar
Gowers, William Timothy and Maurey, Bernard, The unconditional basis problem. Journal of the American Mathematical Society, vol. 6 (1993), no. 4, pp. 851–874.Google Scholar
Hrus̆ák, Michael, Combinatorics of filters and ideals. Contemporary Mathematics, vol. 533 (2011), pp. 29–69.Google Scholar
Neumann, Peter M., Dixon, John D. and Thomas, Simon, Subgroups of small index in infinite symmetric groups. Bulletin of the London Mathematical Society, vol. 18 (1986), no. 6, pp. 207–221.Google Scholar
Just, Winfried and Krawczyk, Adam, On certain Boolean algebras ${\cal P}\left( \omega \right)/I$. Transactions of the American Mathematical Society, vol. 285 (1984), no. 1, pp. 411–429.Google Scholar
Kanovei, Vladimir G., Borel equivalence relations: Structure and classification, University Lecture Series, vol. 44, American Mathematical Society, Providence, RI, 2008.Google Scholar
Kechris, Alexander S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, Berlin, 1995.Google Scholar
Kechris, Alexander S., Rigidity properties of Borel ideals on the integers. Topology and its Applications, vol. 85 (1998), pp. 195–205.Google Scholar
Lang, Serge, Algebra, Graduate Texts in Mathematics, vol. 211, Springer-Verlag, Berlin, 2002.Google Scholar
Lennox, John C. and Robinson, Derek J. S., The theory of infinite soluble groups, Oxford Mathematical Monographs, Oxford University Press, Oxford, UK, 2004.CrossRefGoogle Scholar
Louveau, Alain and Rosendal, Christian, Complete analytic equivalence relations. Transactions of the American Mathematical Society, vol. 357 (2005), no. 12, pp. 4839–4866.Google Scholar
Miller, Arnold W., Countable subgroups of Euclidean space, 2013, preprint, http://arxiv.org/abs/1305.5234.Google Scholar
Moschovakis, Yiannis N., Descriptive set theory, Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar
Munkres, James, Topology, Second ed., Prentice Hall, 2000.Google Scholar
Rosendal, Christian, Cofinal families of Borel equivalence relations and quasiorders, this Journal, vol. 70 (2005), no. 4, pp. 1325–1340.Google Scholar
Rosendal, Christian, Automatic continuity of group homomorphisms. The Bulletin of Symbolic Logic, vol. 15 (2009), no. 2, pp. 184–214.CrossRefGoogle Scholar
Rudin, Mary Ellen, Partial orders on the types in βℕ. Transactions of the American Mathematical Society, vol. 155 (1971), no. 2, pp. 353–362.Google Scholar