Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-28T18:49:16.230Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVERSALLY BAIRE SETS AND GENERIC ABSOLUTENESS

Published online by Cambridge University Press:  09 January 2018

TREVOR M. WILSON
TREVOR M. WILSON*
Affiliation:
DEPARTMENT OF MATHEMATICS MIAMI UNIVERSITY OXFORD, OH45056, USAE-mail:twilson@miamioh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove several equivalences and relative consistency results regarding generic absoluteness beyond Woodin’s 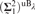${\left( {{\bf{\Sigma }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ generic absoluteness result for a limit of Woodin cardinals λ. In particular, we prove that two-step 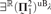$\exists ^ℝ \left( {{\rm{\Pi }}_1^2 } \right)^{{\rm{uB}}_\lambda } $ generic absoluteness below a measurable limit of Woodin cardinals has high consistency strength and is equivalent, modulo small forcing, to the existence of trees for 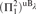${\left( {{\bf{\Pi }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ formulas. The construction of these trees uses a general method for building an absolute complement for a given tree T assuming many “failures of covering” for the models 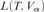$L\left( {T,{V_\alpha }} \right)$ for α below a measurable cardinal.

Keywords

Primary 03E57Secondary 03E1503E55generic absolutenessuniversally BaireWoodin cardinal
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 4 , December 2017 , pp. 1229 - 1251
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., Axioms of generic absoluteness, Logic Colloquium ‘02 (Chatzidakis, Z., Koepke, P., and Pohlers, W., editors), Lecture Notes in Logic, vol. 27, Peters, A K, Natick, MA, 2006, pp. 28–47.Google Scholar
Caicedo, A. E. and Schindler, R., Projective well-orderings of the reals. Archive for Mathematical Logic, vol. 45 (2006), no. 7, pp. 783–793.CrossRefGoogle Scholar
Feng, Q., Magidor, M., and Woodin, W. H., Universally Baire sets of reals, Set Theory of the Continuum (Judah, H., Just, W., and Woodin, W. H., editors), Springer, New York, 1992, pp. 203–242.Google Scholar
Hamkins, J. and Löwe, B., The modal logic of forcing. Transactions of the American Mathematical Society, vol. 360 (2008), no. 4, pp. 1793–1817.Google Scholar
Hamkins, J. D., A simple maximality principle, this Journal, vol. 68 (2003), no. 2, pp. 527–550.Google Scholar
Hauser, K., The consistency strength of projective absoluteness. Annals of Pure and Applied Logic, vol. 74 (1995), no. 3, pp. 245–295.Google Scholar
Kechris, A. S. and Moschovakis, Y. N., Notes on the theory of scales, Games, Scales and Suslin Cardinals: The Cabal Seminar, Volume I (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 31, Cambridge University Press, Cambridge, 2008, pp. 28–74.Google Scholar
Larson, P. B., The Stationary Tower: Notes on a Course by W. Hugh Woodin, University Lecture Series, vol. 32, American Mathematical Society, Providence, RI, 2004.Google Scholar
Martin, D. A. and Woodin, W. H., Weakly homogeneous trees, Games, Scales and Suslin Cardinals: The Cabal Seminar, Volume I (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 31, Cambridge University Press, Cambridge, 2008, pp. 421–438.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar
Neeman, I., Determinacy in L(ℝ), Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Netherlands, 2010, pp. 1887–1950.Google Scholar
Sargsyan, G., Hod mice and the mouse set conjecture. Memoirs of the American Mathematical Society, vol. 236 (2015), no. 1111, pp. 1–172.CrossRefGoogle Scholar
Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable. The Annals of Mathematics, vol. 92 (1970), no. 1, pp. 1–56.Google Scholar
Solovay, R. M., The independence of DC from AD, Cabal Seminar 76–77 (Kechris, A. and Moschovakis, Y., editors), Lecture Notes in Mathematics, vol. 689, Springer, Berlin/Heidelberg, 1978, pp. 171–183.Google Scholar
Steel, J. and Trang, N., AD+, derived models, and ${{\rm{\Sigma }}_1}$ -reflection, preprint, 2010, http://www.math.uci.edu/∼ntrang/AD+reflection.pdf.Google Scholar
Steel, J. R., Derived models associated to mice, Computational Prospects of Infinity (Chong, C. T., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), vol. 14, World Scientific Publishing Company, Singapore, 2008, pp. 105–194.Google Scholar
Steel, J. R., The derived model theorem, Logic Colloquium 2006 (Cooper, S. B., Geuvers, H., Pillay, A., and Väänänen, J., editors), Lecture Notes in Logic, vol. 32, Cambridge University Press, Cambridge, 2009, pp. 280–327.Google Scholar
Wilson, T. M., The envelope of a pointclass under a local determinacy hypothesis. Annals of Pure and Applied Logic, vol. 166 (2015), no. 10, pp. 991–1018.Google Scholar
Wilson, T. M., Scales on ${\rm{\Pi }}_1^2$ sets. Mathematical Research Letters, vol. 22 (2015), no. 1, pp. 301–316.CrossRefGoogle Scholar
Woodin, W. H., On the consistency strength of projective uniformization, Proceedings of the Herbrand Symposium: Logic Colloquium ‘81 (Stern, J., editor), North-Holland, Amsterdam, 1982, pp. 365–384.Google Scholar
Woodin, W. H., Suitable extender models I. Journal of Mathematical Logic, vol. 10 (2010), no. 1,2, pp. 101–339.Google Scholar
Zhu, Y., The derived model theorem II, preprint, 2010, http://wwwmath.uni-muenster.de/logik/Personen/Zhu/der.pdf.Google Scholar