Article contents
Variations on a game of Gale (III): remainder strategies
Published online by Cambridge University Press: 12 March 2014
Extract
An infinite set X is given. D. Gale, in correspondence with J. Mycielski, described the following game in which players one and two play an inning per positive integer: In the nth inning one chooses a finite subset Xn of X, and two chooses a point xn from (X1∪ … ∪Xn)\{x1,…,xn−1}. A play
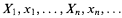
is won by two if  . Gale asked whether two could have a winning strategy which depends for each n on knowledge of only the contents of the set
. Gale asked whether two could have a winning strategy which depends for each n on knowledge of only the contents of the set
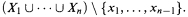
In mathematical terms, is there a function F defined on the collection 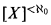 of finite subsets of X such that:
of finite subsets of X such that:
for every sequence X1, x1, …, Xn, xn,…. where each Xn is a finite subset
of X and for each n
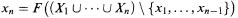
we have 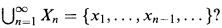
We shall call a strategy of this sort a remainder strategy for two. If there is some finite subset U of X such that F(U) ∉ U, then F cannot be a winning remainder strategy for two, because one can defeat F by choosing U each inning. So, when studying remainder strategies for two we may as well assume that for each finite set U ⊂ X, F(U) ∈ U.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 2
- Cited by

