No CrossRef data available.
Article contents
VARIATIONS ON 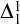 $\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
$\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
Published online by Cambridge University Press: 07 January 2021
Abstract
We consider a seemingly weaker form of 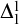 $\Delta ^{1}_{1}$ Turing determinacy.
$\Delta ^{1}_{1}$ Turing determinacy.
Let 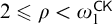 $2 \leqslant \rho < \omega _{1}^{\mathsf {CK}}$,
$2 \leqslant \rho < \omega _{1}^{\mathsf {CK}}$, 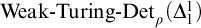 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ is the statement:
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ is the statement:
Every 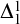 $\Delta ^{1}_{1}$ set of reals cofinal in the Turing degrees contains two Turing distinct,
$\Delta ^{1}_{1}$ set of reals cofinal in the Turing degrees contains two Turing distinct, 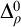 $\Delta ^{0}_{\rho }$-equivalent reals.
$\Delta ^{0}_{\rho }$-equivalent reals.
We show in 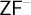 $\mathsf {ZF}^-$:
$\mathsf {ZF}^-$:
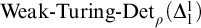 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ implies: for every
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ implies: for every 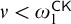 $\nu < \omega _{1}^{\mathsf {CK}}$ there is a transitive model
$\nu < \omega _{1}^{\mathsf {CK}}$ there is a transitive model 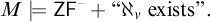 ${M \models \mathsf {ZF}^{-} + \textrm{``}\aleph _{\nu } \textrm{ exists''.}}$
${M \models \mathsf {ZF}^{-} + \textrm{``}\aleph _{\nu } \textrm{ exists''.}}$
As a corollary:
If every cofinal
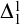 $\Delta ^{1}_{1}$ set of Turing degrees contains both a degree and its jump, then for every
$\Delta ^{1}_{1}$ set of Turing degrees contains both a degree and its jump, then for every 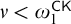 $\nu < \omega_1^{\mathsf{CK}}$, there is atransitive model:
$\nu < \omega_1^{\mathsf{CK}}$, there is atransitive model: 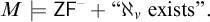 $M \models \mathsf{ZF}^{-} + \textrm{``}\aleph_\nu \textrm{ exists''.}$
$M \models \mathsf{ZF}^{-} + \textrm{``}\aleph_\nu \textrm{ exists''.}$• With a simple proof, this improves upon a well-known result of Harvey Friedman on the strength of Borel determinacy (though not assessed level-by-level).
• Invoking Tony Martin’s proof of Borel determinacy,
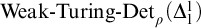 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ implies
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$ implies 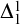 $\Delta ^{1}_{1}$ determinacy.
$\Delta ^{1}_{1}$ determinacy.• We show further that, assuming
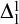 $\Delta ^{1}_{1}$ Turing determinacy, or Borel Turing determinacy, as needed:
$\Delta ^{1}_{1}$ Turing determinacy, or Borel Turing determinacy, as needed:– Every cofinal
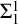 $\Sigma ^{1}_{1}$ set of Turing degrees contains a “hyp-Turing cone”:
$\Sigma ^{1}_{1}$ set of Turing degrees contains a “hyp-Turing cone”: 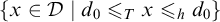 ${\{x \in \mathcal {D} \mid d_{0} \leqslant _{T} x \leqslant _{h} d_{0} \}}$.
${\{x \in \mathcal {D} \mid d_{0} \leqslant _{T} x \leqslant _{h} d_{0} \}}$.– For a sequence
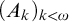 $(A_{k})_{k < \omega }$ of analytic sets of Turing degrees, cofinal in
$(A_{k})_{k < \omega }$ of analytic sets of Turing degrees, cofinal in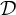 $\mathcal {D}$,
$\mathcal {D}$, 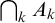 $\bigcap _{k} A_{k}$ is cofinal in
$\bigcap _{k} A_{k}$ is cofinal in 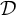 $\mathcal {D}$.
$\mathcal {D}$.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
Footnotes
Presented at the 12th Panhellenic Logic Symposium—Crete, June 2019.


