Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-27T22:38:46.473Z Has data issue: false hasContentIssue false
  • English
  • Français

WAYS OF DESTRUCTION

Part of: Set theory

Published online by Cambridge University Press:  08 October 2021

BARNABÁS FARKAS  and
LYUBOMYR ZDOMSKYY
BARNABÁS FARKAS
Affiliation:
IINSTITUT FÜR DISKRETE MATHEMATIK UND GEOMETRIE TECHNISCHE UNIVERSITÄT WIEN WIEDNER HAUPTSTRASSE 8-10/104 1040WIEN, AUSTRIAE-mail:barnabasfarkas@gmail.comURL: http://dmg.tuwien.ac.at/farkas/E-mail:lzdomsky@gmail.comURL: http://dmg.tuwien.ac.at/zdomskyy/
LYUBOMYR ZDOMSKYY
Affiliation:
IINSTITUT FÜR DISKRETE MATHEMATIK UND GEOMETRIE TECHNISCHE UNIVERSITÄT WIEN WIEDNER HAUPTSTRASSE 8-10/104 1040WIEN, AUSTRIAE-mail:barnabasfarkas@gmail.comURL: http://dmg.tuwien.ac.at/farkas/E-mail:lzdomsky@gmail.comURL: http://dmg.tuwien.ac.at/zdomskyy/
Get access Rights & Permissions [Opens in a new window]

Abstract

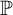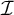We study the following natural strong variant of destroying Borel ideals: $\mathbb {P}$ $+$ -destroys $\mathcal {I}$ if 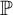$\mathbb {P}$ adds an 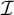$\mathcal {I}$ -positive set which has finite intersection with every 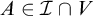$A\in \mathcal {I}\cap V$ . Also, we discuss the associated variants

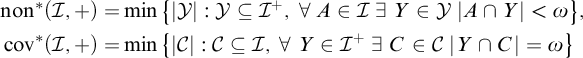$$ \begin{align*} \mathrm{non}^*(\mathcal{I},+)=&\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^+,\; \forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\},\\ \mathrm{cov}^*(\mathcal{I},+)=&\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\; \forall\;Y\in\mathcal{I}^+\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\} \end{align*} $$
of the star-uniformity and the star-covering numbers of these ideals.

Among other results, (1) we give a simple combinatorial characterisation when a real forcing 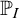$\mathbb {P}_I$ can $+$ -destroy a Borel ideal 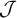$\mathcal {J}$ ; (2) we discuss many classical examples of Borel ideals, their $+$ -destructibility, and cardinal invariants; (3) we show that the Mathias–Prikry, 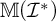$\mathbb {M}(\mathcal {I}^*)$ -generic real $+$ -destroys 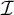$\mathcal {I}$ iff 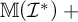$\mathbb {M}(\mathcal {I}^*)\ +$ -destroys 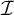$\mathcal {I}$ iff 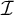$\mathcal {I}$ can be $+$ -destroyed iff $\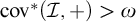mathrm {cov}^*(\mathcal {I},+)>\omega $ ; (4) we characterise when the Laver–Prikry, 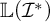$\mathbb {L}(\mathcal {I}^*)$ -generic real $+$ -destroys 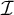$\mathcal {I}$ , and in the case of P-ideals, when exactly 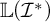$\mathbb {L}(\mathcal {I}^*)$ $+$ -destroys 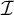$\mathcal {I}$ ; and (5) we briefly discuss an even stronger form of destroying ideals closely related to the additivity of the null ideal.

Keywords

Borel idealMathias–Prikry forcingLaver–Prikry forcingLaflamme’s forcingforcing indestructibilitycovering propertyTukey connectionKatětov orderfragile idealcardinal invariantsBorel Determinacytrace ideal

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E15: Descriptive set theory 03E17: Cardinal characteristics of the continuum 03E35: Consistency and independence results
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 938 - 966
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balcar, B., Hernández-Hernández, F., and Hrušák, M., Combinatorics of dense subsets of the rationals. Fundamenta Mathematicae, vol. 183 (2004), pp. 59–80.10.4064/fm183-1-4CrossRefGoogle Scholar
Balcerzak, M., Farkas, B., and Głab, S., Covering properties of ideals. Archive for Mathematical Logic, vol. 52 (2013), nos. 3–4, pp. 279–294.10.1007/s00153-012-0316-5CrossRefGoogle Scholar
Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line, A. K. Peters, New York, 1995.10.1201/9781439863466CrossRefGoogle Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum, Handbook of Set Theory, vol. 1 (M. Foreman and A. Kanamori, editors), Springer, Berlin, 2010, pp. 395–490.10.1007/978-1-4020-5764-9_7CrossRefGoogle Scholar
Borodulin-Nadzieja, P., Farkas, B., and Plebanek, G., Representation of ideals in polish groups and in Banach spaces, this Journal, vol. 80 (2015), no. 4, pp. 1268–1289.Google Scholar
Brendle, J., Farkas, B., and Verner, J., Towers in filters, cardinal invariants, and Luzin type families, this Journal, vol. 83 (2018), no. 3, pp. 1013–1062.Google Scholar
Brendle, J. and Flašková, J., Generic existence of ultrafilters on the natural numbers. Fundamenta Mathematicae, vol. 236 (2017), pp. 201–245.10.4064/fm730-5-2016CrossRefGoogle Scholar
Brendle, J. and Hrušák, M., Countable Fréchet Boolean groups: An independence result, this Journal, vol. 74 (2009), no. 3, pp. 1061–1068.Google Scholar
Brendle, J. and Yatabe, S., Forcing indestructibility of MAD families. Annals of Pure and Applied Logic, vol. 132 (2005), nos. 2–3, pp. 271–312.10.1016/j.apal.2004.09.002CrossRefGoogle Scholar
Calbrix, J., Classes de Baire et espaces d’applications continues. Comptes Rendus de l'Académie des Sciences—Series I—Mathematics, vol. 301 (1985), pp. 759–762.Google Scholar
Calbrix, J., Filtres Boréliens Sur l’ensemble des entiers et espaces d’applications continues. Revue Roumaine de Mathématique Pures et Appliquées, vol. 33 (1988), pp. 655–661.Google Scholar
Canjar, R. M., Mathias forcing which does not add dominating reals. Proceedings of American Mathematical Society, vol. 104 (1988), no. 4, pp. 1239–1248.10.1090/S0002-9939-1988-0969054-2CrossRefGoogle Scholar
Chodounský, D., Repovš, D., and Zdomskyy, L., Mathias forcing and combinatorial covering properties of filters, this Journal, vol. 80 (2015), no. 4, pp. 1398–1410.Google Scholar
Coskey, S., Mátrai, T., and Steprāns, J., Borel Tukey morphisms and combinatorial cardinal invariants of the continuum. Fundamenta Mathematicae, vol. 223 (2013), pp. 29–48.10.4064/fm223-1-2CrossRefGoogle Scholar
Elekes, M., A covering theorem and the random-indestructibility of the density zero ideal. Real Analysis Exchange, vol. 37 (2011), no. 1, pp. 55–60.10.14321/realanalexch.37.1.0055CrossRefGoogle Scholar
van Engelen, F., On Borel ideals. Annals of Pure and Applied Logic, vol. 70 (1994), pp. 177–203.10.1016/0168-0072(94)90029-9CrossRefGoogle Scholar
Farkas, B., Khomskii, Y., and Vidnyánszky, Z., Almost disjoint refinements and mixing reals. Fundamenta Mathematicae, vol. 242 (2018), pp. 25–48.10.4064/fm429-7-2017CrossRefGoogle Scholar
Farkas, B. and Soukup, L., More on cardinal invariants of analytic P-ideals. Commentationes Mathematicae Universitatis Carolinae, vol. 50 (2009), no. 2, pp. 281–295.Google Scholar
Fremlin, D., Cichoń’s diagram, Séminaire Initiation à l’Analyse (G. Choquet, M. Rogalski, and J. S. Raymond, editors), Publications Mathématiques de l’Université Pierre et Marie Curie, Paris, 1984, pp. 5-01–5-13.Google Scholar
Fremlin, D. H., Measure Theory, Volume 5: Set-Theoretic Measure Theory, Part I, Torres Fremlin, Colchester, 2004.Google Scholar
Hernández-Hernández, F. and Hrušák, M., Cardinal invariants of analytic P-ideals. Canadian Journal of Mathematics, vol. 59 (2007), no. 3, pp. 575–595.10.4153/CJM-2007-024-8CrossRefGoogle Scholar
Hrušák, M., Combinatorics of filters and ideals. Contemporary Mathematics, vol. 533 (2011), pp. 29–69.10.1090/conm/533/10503CrossRefGoogle Scholar
Hrušák, M., Katětov order on Borel ideals. Archive for Mathematical Logic, vol. 56 (2017), nos. 7–8, pp. 831–847.10.1007/s00153-017-0543-xCrossRefGoogle Scholar
Hrušák, M. and Meza-Alcántara, D., Katětov order, Fubini property and Hausdorff ultrafilters. Rendiconti dell'Istituto di Matematica dell'Università di Trieste, vol. 44 (2012), pp. 503–511.Google Scholar
Hrušák, M., Meza-Alcántara, D., and Minami, H., Pair splitting, pair-reaping and cardinal invariants of ${\mathrm{F}}_{\unicode{x3c3}}$ -ideals, this Journal, vol. 75 (2010), no. 2, pp. 661–677.Google Scholar
Hrušák, M., Meza-Alcántara, D., Thümmel, E., and Uzcátegui, C., Ramsey type properties of ideals. Annals of Pure and Applied Logic, vol. 168 (2017), no. 11, pp. 2022–2049.10.1016/j.apal.2017.06.001CrossRefGoogle Scholar
Hrušák, M. and Minami, H., Mathias–Prikry and Laver–Prikry type forcing. Annals of Pure and Applied Logic, vol. 165 (2014), no. 3, pp. 880–894.10.1016/j.apal.2013.11.003CrossRefGoogle Scholar
Hrušák, M. and Zapletal, J., Forcing with quotients. Archive for Mathematical Logic, vol. 47 (2008), pp. 719–739.10.1007/s00153-008-0104-4CrossRefGoogle Scholar
Kanovei, V. and Reeken, M., On Ulam’s problem concerning the stability of approximate homomorphisms. Proceedings of the Steklov Institute of Mathematics, no. 4 (231) (2000), pp. 238–270.Google Scholar
Keremedis, K., On the covering and the additivity number of the real line. Proceedings of the American Mathematical Society, vol. 123 (1995), pp. 1583–1590.10.1090/S0002-9939-1995-1234629-6CrossRefGoogle Scholar
Laflamme, C., Zapping small filters. Proceedings of the American Mathematical Society, vol. 114 (1992), no. 2, pp. 535–544.10.1090/S0002-9939-1992-1068126-5CrossRefGoogle Scholar
Laflamme, C., Filter games and combinatorial properties of strategies, Set Theory (Boise, ID, 1992–1994), (T. Bartoszyński and M. Scheepers, editors) Contemporary Mathematics, vol. 192, American Mathematical Society, Providence, 1996, pp. 51–67.Google Scholar
Laflamme, C. and Leary, C. C., Filter games on $\omega$ and the dual ideal. Fundamenta Mathematicae, vol. 173 (2002), no. 2, pp. 159–173.10.4064/fm173-2-4CrossRefGoogle Scholar
Louveau, A. and Veličković, B., Analytic ideals and cofinal types. Annals of Pure and Applied Logic, vol. 99 (1999), pp. 171–195.CrossRefGoogle Scholar
Martin, D. A., A purely inductive proof of Borel determinacy, Recursion Theory (A. Nerode and R. A. Shore, editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, 1985, pp. 303–308.CrossRefGoogle Scholar
Mazur, K., F ${}_\sigma$ ideals and ${\omega}_1{\omega}_1^{\ast }$ -gaps in the Boolean algebra $\mathcal{P}({\omega})$ /I. Fundamenta Mathematicae, vol. 138 (1991), pp. 103–111.CrossRefGoogle Scholar
Meza-Alcántara, D., Ideals and filters on countable sets, Ph.D. thesis, Universidad Nacional Autónoma de México, 2009.Google Scholar
Solecki, S., Analytic ideals and their applications. Annals of Pure and Applied Logic, vol. 99 (1999), nos. 1–3, pp. 51–72.CrossRefGoogle Scholar
Solecki, S., Filters and sequences. Fundamenta Mathematicae, vol. 163 (2000), no. 3, pp. 215–228.CrossRefGoogle Scholar
Solecki, S. and Todorčević, S., Avoiding families and Tukey functions on the nowhere dense ideal. Journal of the Institute of Mathematics of Jussieu, vol. 10 (2011), pp. 405–435.CrossRefGoogle Scholar
Vojtáš, P., Generalized Galois–Tukey connections between explicit as relations on classical objects of real analysis, Set Theory of the Reals (H. Judah, editor), Israel Mathematical Conference Proceedings, vol. 6, American Mathematical Society, Providence, 1993, pp. 619–643.Google Scholar
Zapletal, J., Forcing Idealized, Cambridge Tracts in Mathematics, vol. 174, Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Zapletal, J., Preserving P-points in definable forcing. Fundamenta Mathematicae, vol. 204 (2009), no. 2, pp. 145–154.CrossRefGoogle Scholar
Zapletal, J., Dimension theory and forcing. Topology and Its Applications, vol. 167 (2014), pp. 31–35.10.1016/j.topol.2014.03.004CrossRefGoogle Scholar