Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:42:40.533Z Has data issue: false hasContentIssue false
  • English
  • Français

Wildness implies undecidability for lattices over group rings

Published online by Cambridge University Press:  12 March 2014

Carlo Toffalori
Carlo Toffalori*
Affiliation:
Dipartimento di Matematica e Fisica, Università di Camerino, Via Madonna Delle Carceri, 62032 Camerino, Italy E-mail: toffalori@camars.unicam.it
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a finite group. A Z [G]-lattice is a finitely generated Z-torsionfree module over the group ring Z [G]. There is a general conjecture concerning classes of modules over sufficiently recursive rings, and linking wildness and undecidability. Given a finite group G, Z [G] is sufficiently recursive, and our aim here is just to investigate this conjecture for Z [G]-lattices. In this setting, the conjecture says that

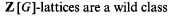
if and only if

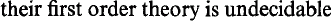
In particular, we wish to deal here with the direction from the left to the right, so the one assuring that wildness implies undecidability. Of course, before beginning the analysis of this problem, one should agree upon a sharp definition of wildness for lattices. But, for our purposes, one might alternatively accept as a starting point a general classification of wild Z [G]-lattices when G is a finite p-group for some prime p, based on the isomorphism type of G. This is due to several authors and can be found, for instance, in [3]. It says that, when p is a prime and G is a finite p-group, then

if and only if

.

More precisely, the representation type of Z [G]-lattices is finite when G is cyclic of order ≤ p2, tame domestic when G is the Klein group [1], tame non-domestic when G is cyclic of order 8 [11].

So our claim might be stated as follows.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1429 - 1447
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Butler, M., The 2-adic representations of Klein's four group, Proceedings 2nd International Conference on the Theory of Groups, Lecture Notes in Mathematics, vol. 372, Springer-Verlag, Berlin, 1974, pp. 197–203.Google Scholar
[2]Curtis, C. and Reiner, I., Methods of representation theory with applications to finite groups and orders, vol. 1, Wiley, New York, 1981.Google Scholar
[3]Dieterich, E., Group rings of wild representation type, Mathematische Annalen, vol. 266 (1983), pp. 1–22.CrossRefGoogle Scholar
[4]Green, E. and Reiner, I., Integral representations and diagrams, Michigan Journal of Mathematics, vol. 25 (1978), pp. 53–84.CrossRefGoogle Scholar
[5]Marcja, A. and Toffalori, C., Decidable representations, Journal of Pure and Applied Algebra, vol. 103 (1995), pp. 189–203.CrossRefGoogle Scholar
[6]Prest, M., Model theory and modules, London Mathematical Society Lecture Notes Series, vol. 130, Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
[7]Ringel, C. and Roggenkamp, K., Diagrammatic methods in the representation theory of orders, Journal of Algebra, vol. 60 (1979), pp. 11–42.CrossRefGoogle Scholar
[8]Toffalori, C., The decision problem for ZsC(p 3)-lattices with p prime, preprint.Google Scholar
[9]Toffalori, C., An undecidability theorem for lattices over group rings, Annals of Pure and Applied Logic, to appear.Google Scholar
[10]Toffalori, C., Two questions concerning decidability for lattices over a group ring, Unione Matematica Italiana, Bollettino, vol. 10-B (1996), pp. 799–814.Google Scholar
[11]Yakovlev, A., Classification of 2-adic representations of an eighth order cyclic group, Zap. Nauc. Sem. Leningrad. Otd. Mat. Inst. Steklov (LOMI), vol. 28 (1972), pp. 93–129, Soviet Math., vol. 3 (1975), pp. 654–680.Google Scholar