1.1 The system K* of basic logic, as presented in a previous paper, will be shown to be formalizable in an alternative way according to which the rule [E],
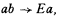
is replaced by the rule [F],
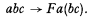
1.2. General recursive functions will be shown to be definable in K* in a way that retains functional notation, so that the equation,
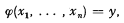
will be formalized in K* by the formula,
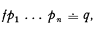
where ‘f’, ‘p1’, … ‘pn’ respectively denote φ, x1, …, xn, and where ‘≐’ plays the role of numerical equality. Partial recursive functions may be handled in a similar way. The rule [E] is not required for dealing with primitive recursive functions by this method.
1.3. An operator ‘G’ will be defined such that ‘[Ga ≐ p]’ is a theorem of K* if and only if ‘p’ denotes the Gödel number of ‘a’.
1.4. In reformulating K* we assume ‘o0’, ‘o1,’ ‘o2’, …, have been so chosen that we can determine effectively whether or not a given U-expression is the mth member of the above series. The revised rules for K* are then as follows. (Double-arrow forms of these rules are derivable, except in the case of rule [V].)