Article contents
CAYLEY–ABELS GRAPHS AND INVARIANTS OF TOTALLY DISCONNECTED, LOCALLY COMPACT GROUPS
Published online by Cambridge University Press: 13 April 2022
Abstract
A connected, locally finite graph 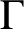 $\Gamma $ is a Cayley–Abels graph for a totally disconnected, locally compact group G if G acts vertex-transitively on
$\Gamma $ is a Cayley–Abels graph for a totally disconnected, locally compact group G if G acts vertex-transitively on 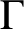 $\Gamma $ with compact, open vertex stabilizers. Define the minimal degree of G as the minimal degree of a Cayley–Abels graph of G. We relate the minimal degree in various ways to the modular function, the scale function and the structure of compact open subgroups. As an application, we prove that if
$\Gamma $ with compact, open vertex stabilizers. Define the minimal degree of G as the minimal degree of a Cayley–Abels graph of G. We relate the minimal degree in various ways to the modular function, the scale function and the structure of compact open subgroups. As an application, we prove that if 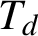 $T_{d}$ denotes the d-regular tree, then the minimal degree of
$T_{d}$ denotes the d-regular tree, then the minimal degree of 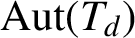 $\mathrm{Aut}(T_{d})$ is d for all
$\mathrm{Aut}(T_{d})$ is d for all 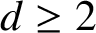 $d\geq 2$.
$d\geq 2$.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by George Willis
The second named author was supported by Early Postdoc. Mobility scholarship No. 175106 from the Swiss National Science Foundation. Part of this work was done when she was visiting the University of Newcastle with the International Visitor Program of the Sydney Mathematical Research Institute.
References
- 1
- Cited by


