Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T16:02:07.448Z Has data issue: false hasContentIssue false
  • English
  • Français

FACTORIZING MULTILINEAR KERNEL OPERATORS THROUGH SPACES OF VECTOR MEASURES

Part of: Harmonic analysis in several variables Measures, integration, derivative, holomorphy

Published online by Cambridge University Press:  13 January 2020

ORLANDO GALDAMES-BRAVO
ORLANDO GALDAMES-BRAVO*
Affiliation:
Departament de Matemàtiques, Universitat de València, 46100 Burjassot, València, Spain e-mail: orlando.galdames@uv.es
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a multilinear kernel operator between Banach function spaces over finite measures and suitable order continuity properties, namely 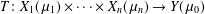$T:X_{1}(\,\unicode[STIX]{x1D707}_{1})\times \cdots \times X_{n}(\,\unicode[STIX]{x1D707}_{n})\rightarrow Y(\,\unicode[STIX]{x1D707}_{0})$. Then we define, via duality, a class of linear operators associated to the 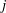$j$-transpose operators. We show that, under certain conditions of 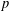$p$th power factorability of such operators, there exist vector measures 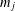$m_{j}$ for 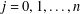$j=0,1,\ldots ,n$ so that 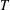$T$ factors through a multilinear operator 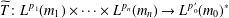$\widetilde{T}:L^{p_{1}}(m_{1})\times \cdots \times L^{p_{n}}(m_{n})\rightarrow L^{p_{0}^{\prime }}(m_{0})^{\ast }$, provided that 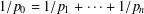$1/p_{0}=1/p_{1}+\cdots +1/p_{n}$. We apply this scheme to the study of the class of multilinear Calderón–Zygmund operators and provide some concrete examples for the homogeneous polynomial and multilinear Volterra and Laplace operators.

Keywords

multilinear Calderón–Zygmund operatorpth power factorable operatorvector measure

MSC classification

Primary: 46G10: Vector-valued measures and integration
Secondary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 1 , February 2022 , pp. 30 - 51
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by C. Meaney

References

Achour, D., Dahia, E., Rueda, P. and Sánchez-Pérez, E. A., ‘Domination spaces and factorization of linear and multilinear summing operators’, Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. RACSAM 39(8) (2016), 1071–1092.Google Scholar
Calabuig, J. M., Fernández-Unzueta, M., Galaz-Fontes, F. and Sánchez-Pérez, E. A., ‘Extending and factorizing bounded bilinear maps defined on order continuous Banach function spaces’, Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. RACSAM 108(2) (2014), 353–367.CrossRefGoogle Scholar
Calderón, A. and Zygmund, A., ‘On the existence of certain singular integrals’, Acta Math. 88 (1952), 85–139.CrossRefGoogle Scholar
Coifman, R. R. and Meyer, Y., ‘On commutators of singular integrals and bilinear singular integrals’, Trans. Amer. Math. Soc. 212 (1975), 315–331.CrossRefGoogle Scholar
Curbera, G. P., García-Cuerva, J., Martell, J. M. and Pérez, C., ‘Extrapolation with weights to rearrangement invariant function spaces and modular inequalities, with applications to singular integrals’, Adv. Math. 203 (2006), 256–318.CrossRefGoogle Scholar
Defant, A. and Floret, K., Tensor Norms and Operator Ideals, Mathematics Studies, 176 (North-Holland, Amsterdam, 1993).Google Scholar
Diestel, J. and Uhl, J. J. Jr, Vector Measures (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
Fernández, A., Mayoral, F., Naranjo, F., Sáez, C. and Sánchez-Pérez, E. A., ‘Spaces of integrable functions with respect to a vector measure and factorizations through L p and Hilbert spaces’, J. Math. Anal. Appl. 330 (2007), 1249–1263.CrossRefGoogle Scholar
Galdames-Bravo, O., ‘On the optimal domain of the Laplace transform’, Bull. Malays. Math. Sci. Soc. 40(1) (2017), 389–408.CrossRefGoogle Scholar
Galdames-Bravo, O., ‘Extrapolation theorems for (p, q)-factorable operators’, Banach J. Math. Anal. 12(2) (2018), 497–514.CrossRefGoogle Scholar
Galdames-Bravo, O. and Sánchez-Pérez, E. A., ‘Factorizing kernel operators’, Integral Equations Operator Theory 75 (2013), 13–29.CrossRefGoogle Scholar
Grafakos, L. and Torres, R. H., ‘Multilinear Calderón–Zygmund theory’, Adv. Math. 165 (2002), 124–164.CrossRefGoogle Scholar
Lerner, A. K., Ombrosi, S., Pérez, C., Torres, R. H. and Trujillo-González, R., ‘New maximal functions and multiple weights for the multilinear Calderón–Zygmund theory’, Adv. Math. 220 (2009), 1222–1264.CrossRefGoogle Scholar
Li, W., Xue, Q. and Yabuta, K., ‘Multilinear Calderón–Zygmund operators on weighted Hardy spaces’, Studia Math. 108(1) (2010), 1–16.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces II (Springer, Berlin, 1979).CrossRefGoogle Scholar
Lu, G. and Zhang, P., ‘Multilinear Calderón–Zygmund operators with kernels of Dini’s type and applications’, Nonlinear Anal. 107 (2014), 92–117.CrossRefGoogle Scholar
Lu, Y. and Ping, Z. Y., ‘Boundedness of multilinear Calderón–Zygmund singular operators on Morrey–Herz spaces with variable exponents’, Acta Math. Sin. (Engl. Ser.) 30(7) (2014), 1180–1194.CrossRefGoogle Scholar
Oberlin, D. M., ‘A multilinear Young’s inequality’, Canad. Math. Bull. 33(3) (1988), 380–384.CrossRefGoogle Scholar
Okada, S., Ricker, W. J. and Sánchez-Pérez, E. A., Optimal Domain and Integral Extension of Operators Acting in Function Spaces, Operator Theory: Advances and Applications, 180 (Birkhäuser, Basel, 2008).CrossRefGoogle Scholar
Rugh, W. J., Nonlinear System Theory: The Volterra/Wiener Approach (The Johns Hopkins University Press, Baltimore, MD, 1981).Google Scholar
Stein, E. M., Harmonic Analysis: Real Variable Methods, Orthogonality and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Yilmaz, H., ‘Wave functions and transition probabilities for light atoms’, Phys. Rev. 100(4) (1955), 1148–1153.CrossRefGoogle Scholar