Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T03:52:37.019Z Has data issue: false hasContentIssue false
  • English
  • Français

GRAPH IMMERSIONS, INVERSE MONOIDS AND DECK TRANSFORMATIONS

Part of: Low-dimensional topology Semigroups

Published online by Cambridge University Press:  02 March 2020

CORBIN GROOTHUIS  and
JOHN MEAKIN
CORBIN GROOTHUIS
Affiliation:
Department of Mathematics, University of Nebraska, Lincoln, NE68588, USA e-mail: corbin.groothuis@huskers.unl.edu
JOHN MEAKIN*
Affiliation:
Department of Mathematics, University of Nebraska, Lincoln, NE68588, USA
*
e-mail: jmeakin@unl.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

If 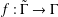$f:\tilde{\unicode[STIX]{x1D6E4}}\rightarrow \unicode[STIX]{x1D6E4}$ is a covering map between connected graphs, and 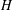$H$ is the subgroup of 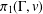$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6E4},v)$ used to construct the cover, then it is well known that the group of deck transformations of the cover is isomorphic to 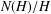$N(H)/H$, where 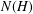$N(H)$ is the normalizer of 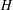$H$ in 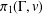$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6E4},v)$. We show that an entirely analogous result holds for immersions between connected graphs, where the subgroup 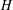$H$ is replaced by the closed inverse submonoid of the inverse monoid 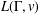$L(\unicode[STIX]{x1D6E4},v)$ used to construct the immersion. We observe a relationship between group actions on graphs and deck transformations of graph immersions. We also show that a graph immersion 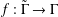$f:\tilde{\unicode[STIX]{x1D6E4}}\rightarrow \unicode[STIX]{x1D6E4}$ may be extended to a cover 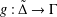$g:\tilde{\unicode[STIX]{x1D6E5}}\rightarrow \unicode[STIX]{x1D6E4}$ in such a way that all deck transformations of 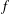$f$ are restrictions of deck transformations of 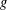$g$.

Keywords

graph immersiondeck transformationfree inverse monoid

MSC classification

Primary: 20M18: Inverse semigroups
Secondary: 57M10: Covering spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 1 , August 2021 , pp. 37 - 55
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by B. Martin

References

Birget, J.-C., Margolis, S., Meakin, J. and Weil, P., ‘PSPACE-complete problems for subgroups of free groups and inverse finite automata’, Theor. Comput. Sci. 242(1–2) (2000), 247–281.Google Scholar
Gluskin, L. M., ‘Elementary generalized groups’, Mat. Sb. 41 (1957), 23–36 (in Russian).Google Scholar
Hatcher, A., Algebraic Topology (Cambridge University Press, Cambridge, 2001).Google Scholar
Kapovich, I. and Myasnikov, A., ‘Stallings foldings and subgroups of free groups’, J. Algebra 248 (2002), 608–668.Google Scholar
Lawson, M. V., Inverse Semigroups: The Theory of Partial Symmetries (World Scientific, Singapore, 1998).Google Scholar
Lawson, M. V., Margolis, S. W. and Steinberg, B., ‘The étale groupoid of an inverse semigroup as a groupoid of filters’, J. Aust. Math. Soc. 94 (2013), 234–256.Google Scholar
Margolis, S. and Meakin, J., ‘Free inverse monoids and graph immersions’, Internat. J. Algebra Comput. 3(1) (1993), 79–99.Google Scholar
McAlister, D. B., ‘Groups, semilattices and inverse semigroups II’, Trans. Amer. Math. Soc. 196 (1974), 251–270.Google Scholar
Meakin, J. and Szakács, N., ‘Inverse monoids and immersions of 2-complexes’, Internat. J. Algebra Comput. 25(1–2) (2015), 301–324.Google Scholar
Meakin, J. and Szakács, N., ‘Inverse monoids and immersions of cell complexes’, Preprint, 2017, arXiv:1709.03887.Google Scholar
Munn, W. D., ‘Free inverse semigroups’, Proc. Lond. Math. Soc. (3) 29 (1974), 385–404.Google Scholar
Petrich, M., Inverse Semigroups (Wiley, New York, 1984).Google Scholar
Scheiblich, H. E., ‘Free inverse semigroups’, Proc. Amer. Math. Soc. 38 (1973), 1–7.Google Scholar
Schein, B. M., ‘Representations of generalized groups’, Izv. Vyssh. Uchebn. Zaved. Mat. 3 (1962), 164–176 (in Russian).Google Scholar
Serre, J. P., Trees (Springer, New York, 1980).Google Scholar
Stallings, J. R., ‘Topology of finite graphs’, Invent. Math. 71(3) (1983), 551–565.Google Scholar
Stephen, J. B., ‘Presentations of inverse monoids’, J. Pure Appl. Algebra 63 (1990), 81–112.Google Scholar