Published online by Cambridge University Press: 12 September 2022
In this paper, we show that Leavitt path algebras of weighted graphs and Leavitt path algebras of separated graphs are intimately related. We prove that any Leavitt path algebra 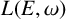 $L(E,\omega )$ of a row-finite vertex weighted graph
$L(E,\omega )$ of a row-finite vertex weighted graph 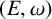 $(E,\omega )$ is
$(E,\omega )$ is  $*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph
$*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph 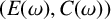 $(E(\omega ),C(\omega ))$. For a general locally finite weighted graph
$(E(\omega ),C(\omega ))$. For a general locally finite weighted graph 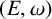 $(E, \omega )$, we show that a certain quotient
$(E, \omega )$, we show that a certain quotient 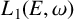 $L_1(E,\omega )$ of
$L_1(E,\omega )$ of 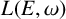 $L(E,\omega )$ is
$L(E,\omega )$ is  $*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph
$*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph 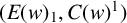 $(E(w)_1,C(w)^1)$. We furthermore introduce the algebra
$(E(w)_1,C(w)^1)$. We furthermore introduce the algebra 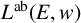 ${L^{\mathrm {ab}}} (E,w)$, which is a universal tame
${L^{\mathrm {ab}}} (E,w)$, which is a universal tame  $*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of
$*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of 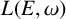 $L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra
$L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra 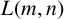 $L(m,n)$.
$L(m,n)$.
Communicated by Daniel Chan
Partially supported by DGI-MINECO-FEDER grant PID2020-113047GB-I00, and the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (CEX2020-001084-M).