No CrossRef data available.
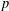 $p$-ADIC NUMBERS
$p$-ADIC NUMBERSPublished online by Cambridge University Press: 12 December 2019
We carry Sprindžuk’s classification of the complex numbers to the field 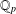 $\mathbb{Q}_{p}$ of
$\mathbb{Q}_{p}$ of 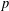 $p$-adic numbers. We establish several estimates for the
$p$-adic numbers. We establish several estimates for the 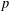 $p$-adic distance between
$p$-adic distance between 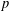 $p$-adic roots of integer polynomials, which we apply to show that almost all
$p$-adic roots of integer polynomials, which we apply to show that almost all 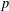 $p$-adic numbers, with respect to the Haar measure, are
$p$-adic numbers, with respect to the Haar measure, are 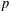 $p$-adic
$p$-adic 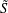 $\tilde{S}$-numbers of order 1.
$\tilde{S}$-numbers of order 1.
Communicated by M. Coons
This research was supported by the Scientific Research Projects Coordination Unit of Istanbul University (project number FUA-2018-31152).