Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T08:49:54.189Z Has data issue: false hasContentIssue false
  • English
  • Français

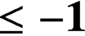REALIZING METRICS OF CURVATURE $\mathbf {\leq -1}$ ON CLOSED SURFACES IN FUCHSIAN ANTI-DE SITTER MANIFOLDS

Part of: Global differential geometry

Published online by Cambridge University Press:  19 February 2021

HICHAM LABENI Open the ORCID record for HICHAM LABENI [Opens in a new window]
HICHAM LABENI*
Affiliation:
CY Cergy Paris Université, Laboratoire AGM, UMR 8088 du CNRS, F-95000Cergy, France
*
e-mail: hicham.labeni@cyu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any metric with curvature less than or equal to 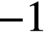$-1$ (in the sense of A. D. Alexandrov) on a closed surface of genus greater than 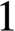$1$ is isometric to the induced intrinsic metric on a space-like convex surface in a Lorentzian manifold of dimension 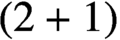$(2+1)$ with sectional curvature 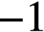$-1$ . The proof is by approximation, using a result about isometric immersion of smooth metrics by Labourie and Schlenker.

Keywords

anti-de SitterCAT(-1)Fuchsian surfaces

MSC classification

Primary: 53C45: Global surface theory (convex surfaces à la A. D. Aleksandrov)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 3 , June 2022 , pp. 312 - 334
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Graeme Wilkin

The author was supported by: École Doctorale Économie, Management, Mathématiques, Physique et Sciences Informatiques (EM2PSI)ED no 405 – CY Cergy Paris Université.

References

Aleksandrov, A. D. and Zalgaller, V. A., Intrinsic Geometry of Surfaces, translated from the Russian by Danskin, J. M.. Translations of Mathematical Monographs, 15 (American Mathematical Society, Providence, RI, 1967).Google Scholar
Alexandrov, A. D., A. D. Alexandrov Selected Works. Part II: Intrinsic Geometry of Convex Surfaces (ed. Kutateladze, S. S.), translated from the Russian by Vakhrameyev, S. (Chapman & Hall/CRC, Boca Raton, FL, 2006).Google Scholar
Bonsante, F. and Schlenker, J.-M., ‘Maximal surfaces and the universal Teichmüller space’, Invent. Math. 182(2) (2010), 279–333.CrossRefGoogle Scholar
Bonsante, F. and Schlenker, J.-M., ‘Fixed points of compositions of earthquakes’, Duke Math. J. 161(6) (2012), 1011–1054.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A., Metric Spaces of Non-Positive Curvature, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319 (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Burago, D., Burago, Y. and Ivanov, S., A Course in Metric Geometry, Graduate Studies in Mathematics, 33 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Burtscher, A. Y., ‘Length structures on manifolds with continuous Riemannian metrics’, New York J. Math. 21 (2015), 273–296.Google Scholar
Buser, P., Geometry and Spectra of Compact Riemann Surfaces, Modern Birkhäuser Classics, Reprint of the 1992 edition (Birkhäuser, Boston, 2010).CrossRefGoogle Scholar
Fillastre, F., Izmestiev, I. and Veronelli, G., ‘Hyperbolization of cusps with convex boundary’, Manuscripta Math. 150(3–4) (2016), 475–492.CrossRefGoogle Scholar
Fillastre, F. and Slutskiy, D., ‘Embeddings of non-positively curved compact surfaces in flat Lorentzian manifolds’, Math. Z. 291(1–2) (2019), 149–178.CrossRefGoogle Scholar
Labourie, F. and Schlenker, J.-M., ‘Surfaces convexes fuchsiennes dans les espaces lorentziens à courbure constante’, Math. Ann. 316(3) (2000), 465–483.CrossRefGoogle Scholar
Mess, G., ‘Lorentz spacetimes of constant curvature’, Geom. Dedicata 126 (2007), 3–45.CrossRefGoogle Scholar
Mumford, D., ‘A remark on Mahler’s compactness theorem’, Proc. Amer. Math. Soc. 28 (1971), 289–294.Google Scholar
O’Neill, B., Semi-Riemannian Geometry with Applications to Relativity, Pure and Applied Mathematics, 103 (Harcourt Brace Jovanovich, New York, 1983).Google Scholar
Slutsky, D., ‘Métriques polyèdrales sur les bords de variétés hyperboliques convexes et flexibilité des polyèdres hyperboliques’, PhD Thesis, Université Toulouse III Paul Sabatier, 2013.Google Scholar
Tyrrell Rockafellar, R., Convex Analysis, Princeton Landmarks in Mathematics, Reprint of the 1970 original, Princeton Paperbacks (Princeton University Press, Princeton, NJ, 1997).Google Scholar