No CrossRef data available.
Article contents
SIMPLICITY OF CROSSED PRODUCTS BY TWISTED PARTIAL ACTIONS
Part of:
Selfadjoint operator algebras
Topological dynamics
Smooth dynamical systems: general theory
Rings and algebras with additional structure
Rings and algebras arising under various constructions
Published online by Cambridge University Press: 08 April 2019
Abstract
In this article, we consider a twisted partial action 
$\unicode[STIX]{x1D6FC}$ of a group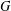 
$G$ on an associative ring 
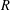$R$ and its associated partial crossed product 
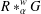$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$. We provide necessary and sufficient conditions for the commutativity of 
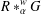$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ when the twisted partial action 
$\unicode[STIX]{x1D6FC}$ is unital. Moreover, we study necessary and sufficient conditions for the simplicity of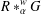 
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ in the following cases: (i) 
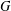$G$ is abelian; (ii) 
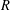$R$ is maximal commutative in 
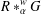$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$; (iii) 
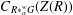$C_{R\ast _{\unicode[STIX]{x1D6FC}}^{w}G}(Z(R))$ is simple; (iv) 
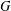$G$ is hypercentral. When 
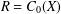$R=C_{0}(X)$ is the algebra of continuous functions defined on a locally compact and Hausdorff space 
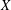$X$, with complex values that vanish at infinity, and 
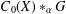$C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ is the associated partial skew group ring of a partial action 
$\unicode[STIX]{x1D6FC}$ of a topological group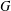 
$G$ on 
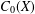$C_{0}(X)$, we study the simplicity of 
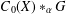$C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ by using topological properties of 
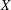$X$ and the results about the simplicity of 
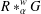$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
Abadie, F., ‘Enveloping actions and Takai duality for partial actions’, J. Funct. Anal. 197 (2003), 14–67.Google Scholar
Batista, E., Alves, M. M. S., Dokuchaev, M. and Paques, A., ‘Twisted partial actions of Hopf algebras’, Israel J. Math. 197 (2013), 263–308.Google Scholar
Batista, E., Alves, M. M. S., Dokuchaev, M. and Paques, A., ‘Globalization of twisted partial Hopf actions’, J. Aust. Math. Soc. 101 (2016), 1–28.Google Scholar
Caenepeel, S. and Janssen, K., ‘Partial (co)actions of Hopf algebras and partial Hopf–Galois theory’, Comm. Algebra 36 (2008), 2923–2946.Google Scholar
Cortes, W., Ferrero, M. and Gobbi, L., ‘Quasi-duo partial skew polynomial rings’, Algebra Discrete Math. 12 (2011), 53–63.Google Scholar
Della Flora, S. S., ‘Sobre ações parciais torcidas de grupos e o produto cruzado parcial’, PhD Thesis, Universidade Federal do Rio Grande do Sul, 2012.Google Scholar
Dokuchaev, M. and Exel, R., ‘Associativity of crossed products by partial actions, enveloping actions and partial representations’, Trans. Amer. Math. Soc. 357(5) (2005), 1931–1952.Google Scholar
Dokuchaev, M., Exel, R. and Simón, J. J., ‘Crossed products by twisted partial actions and graded algebras’, J. Algebra 320 (2008), 3278–3310.Google Scholar
Dokuchaev, M., Exel, R. and Simón, J. J., ‘Globalization of twisted partial actions’, Trans. Amer. Math. Soc. 362 (2010), 4137–4160.Google Scholar
Dokuchaev, M., Ferrero, M. and Paques, A., ‘Partial actions and Galois theory’, J. Pure Appl. Algebra 208(1) (2007), 77–87.Google Scholar
Exel, R., ‘Twisted partial actions: a classification of regular C ∗ -algebraic bundles’, Proc. Lond. Math. Soc. 74 (1997), 417–443.Google Scholar
Exel, R., ‘Hecke algebras for protonormal subgroups’, J. Algebra 320 (2008), 1771–1813.Google Scholar
Exel, R., Laca, M. and Quigg, J., ‘Partial dynamical system and C ∗ -algebras generated by partial isometries’, J. Operator Theory 47 (2002), 169–186.Google Scholar
Ferrero, M. and Lazzarin, J., ‘Partial actions and partial skew group rings’, J. Algebra 139 (2008), 5247–5264.Google Scholar
Gonçalves, D., ‘Simplicity of partial skew group rings of abelian groups’, Canad. Math. Bull. 57 (2014), 511–519.Google Scholar
Gonçalves, D., Oinert, J. and Royer, D., ‘Simplicity of partial skew group rings with applications to Leavitt path algebras and topological dynamics’, J. Algebra 420 (2014), 201–216.Google Scholar
Jespers, E., ‘Simple abelian-group graded rings’, Boll. Unione Mat. Ital. 3‐A(7) (1989), 103–106.Google Scholar
Lundström, P. and Öinert, J., ‘The ideal intersection property for groupoid graded rings’, Comm. Algebra 40 (2012), 1860–1871.Google Scholar
McClanahan, K., ‘K-theory for partial crossed products by discrete groups’, J. Funct. Anal. 130 (1995), 77–117.Google Scholar
McLain, D. H., ‘Remarks on the upper central series of a group’, Proc. Glasg. Math. Assoc. 3 (1956), 38–44.Google Scholar
Nystedt, P. and Oinert, J., ‘Simple semigroup graded rings’, J. Algebra Appl. 14 (2015), 1550102.Google Scholar
Oinert, J., ‘Simple group graded rings and maximal commutativity’, Contemp. Math. 503 (2009), 159–175.Google Scholar
Oinert, J., ‘Simplicity of skew group rings of abelian groups’, Comm. Algebra 42 (2014), 821–841.Google Scholar
Paques, A. and Sant’Ana, A., ‘When is a crossed product by a twisted partial action Azumaya?’, Comm. Algebra 38 (2010), 1093–1103.Google Scholar
Quigg, J. C. and Raeburn, I., ‘Characterizations of crossed products by partial actions’, J. Operator Theory 37 (1997), 311–340.Google Scholar
Svensson, C., Silvestrov, S. and de Jeu, M., ‘Dynamical systems and commutants in crossed products’, Internat. J. Math. 18 (2007), 455–471.Google Scholar