Hostname: page-component-7dd5485656-s6l46 Total loading time: 0 Render date: 2025-10-29T10:10:06.072Z Has data issue: false hasContentIssue false
  • English
  • Français

SMALL-BOUND ISOMORPHISMS OF FUNCTION SPACES

Part of: Special classes of linear operators Topological linear spaces and related structures

Published online by Cambridge University Press:  18 March 2020

JAKUB RONDOŠ Open the ORCID record for JAKUB RONDOŠ [Opens in a new window]  and
JIŘÍ SPURNÝ
JAKUB RONDOŠ*
Affiliation:
Charles University, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Sokolovská 83, 186 75 Praha 8, Czech Republic
JIŘÍ SPURNÝ
Affiliation:
Charles University, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Sokolovská 83, 186 75 Praha 8, Czech Republic e-mail: spurny@karlin.mff.cuni.cz
*
e-mail: jakub.rondos@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 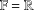$\mathbb{F}=\mathbb{R}$ or 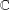$\mathbb{C}$. For 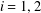$i=1,2$, let 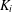$K_{i}$ be a locally compact (Hausdorff) topological space and let 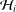${\mathcal{H}}_{i}$ be a closed subspace of 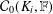${\mathcal{C}}_{0}(K_{i},\mathbb{F})$ such that each point of the Choquet boundary 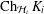$\operatorname{Ch}_{{\mathcal{H}}_{i}}K_{i}$ of 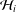${\mathcal{H}}_{i}$ is a weak peak point. We show that if there exists an isomorphism $T:{\mathcal{H}}_{1}\rightarrow {\mathcal{H}}_{2}$ with 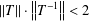$\left\Vert T\right\Vert \cdot \left\Vert T^{-1}\right\Vert <2$, then 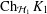$\operatorname{Ch}_{{\mathcal{H}}_{1}}K_{1}$ is homeomorphic to 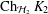$\operatorname{Ch}_{{\mathcal{H}}_{2}}K_{2}$. We then provide a one-sided version of this result. Finally we prove that under the assumption on weak peak points the Choquet boundaries have the same cardinality provided 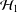${\mathcal{H}}_{1}$ is isomorphic to 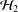${\mathcal{H}}_{2}$.

Keywords

function spaceBanach–Stone theoremCambern theorem

MSC classification

Primary: 47B38: Operators on function spaces (general) 46A55: Convex sets in topological linear spaces; Choquet theory

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 3 , December 2021 , pp. 412 - 429
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by A. Sims

The research was supported by the research grant GAČR 17-00941S.

References

Al-Halees, H. and Fleming, R. J., ‘Isomorphic vector-valued Banach–Stone theorems for subspaces’, Acta Sci. Math. (Szeged) 81(1–2) (2015), 189–214.10.14232/actasm-014-255-xCrossRefGoogle Scholar
Alfsen, E. M., Compact Convex Sets and Boundary Integrals, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 57 (Springer, New York, 1971).10.1007/978-3-642-65009-3CrossRefGoogle Scholar
Amir, D., ‘On isomorphisms of continuous function spaces’, Israel J. Math. 3 (1965), 205–210.10.1007/BF03008398CrossRefGoogle Scholar
Batty, C. J. K., ‘Vector-valued Choquet theory and transference of boundary measures’, Proc. Lond. Math. Soc. (3) 60(3) (1990), 530–548.10.1112/plms/s3-60.3.530CrossRefGoogle Scholar
Behrends, E., M-Structure and the Banach–Stone Theorem, Lecture Notes in Mathematics, 736 (Springer, Berlin, 1979).10.1007/BFb0063153CrossRefGoogle Scholar
Behrends, E. and Cambern, M., ‘An isomorphic Banach–Stone theorem’, Studia Math. 90(1) (1988), 15–26.10.4064/sm-90-1-15-26CrossRefGoogle Scholar
Cambern, M., ‘A generalized Banach–Stone theorem’, Proc. Amer. Math. Soc. 17 (1966), 396–400.10.1090/S0002-9939-1966-0196471-9CrossRefGoogle Scholar
Cambern, M., ‘Isomorphisms of spaces of continuous vector-valued functions’, Illinois J. Math. 20(1) (1976), 1–11.10.1215/ijm/1256050155CrossRefGoogle Scholar
Cengiz, B., ‘On topological isomorphisms of C 0(X) and the cardinal number of X ’, Proc. Amer. Math. Soc. 72(1) (1978), 105–108.Google Scholar
Chu, C. H. and Cohen, H. B., ‘Isomorphisms of spaces of continuous affine functions’, Pacific J. Math. 155(1) (1992), 71–85.10.2140/pjm.1992.155.71CrossRefGoogle Scholar
Cohen, H. B., ‘A bound-two isomorphism between C (X) Banach spaces’, Proc. Amer. Math. Soc. 50 (1975), 215–217.Google Scholar
Cohen, H. B., ‘A second-dual method for C (X) isomorphisms’, J. Funct. Anal. 23(2) (1976), 107–118.10.1016/0022-1236(76)90069-0CrossRefGoogle Scholar
Dostál, P. and Spurný, J., ‘The minimum principle for affine functions and isomorphisms of continuous affine function spaces’, Arch. Math. 114(1) (2020), 61–70.10.1007/s00013-019-01371-0CrossRefGoogle Scholar
Drewnowski, L., ‘A remark on the Amir–Cambern theorem’, Funct. Approx. Comment. Math. 16 (1988), 181–190.Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V. and Zizler, V., Banach Space Theory: The Basis for Linear and Nonlinear Analysis, CMS Books in Mathematics (Springer, New York, 2011).10.1007/978-1-4419-7515-7CrossRefGoogle Scholar
Fleming, R. J. and Jamison, J. E., Isometries on Banach Spaces: Function Spaces, Chapman and Hall/CRC Monographs and Surveys in Pure and Applied Mathematics, 129 (Chapman and Hall/CRC, Boca Raton, FL, 2003).Google Scholar
Fleming, R. J. and Jamison, J. E., ‘Isometries on Banach spaces’, in: Vector-Valued Function Spaces, Chapman and Hall/CRC Monographs and Surveys in Pure and Applied Mathematics, 138 (Chapman and Hall/CRC, Boca Raton, FL, 2008).Google Scholar
Fuhr, R. and Phelps, R. R., ‘Uniqueness of complex representing measures on the Choquet boundary’, J. Funct. Anal. 14 (1973), 1–27.10.1016/0022-1236(73)90027-XCrossRefGoogle Scholar
Galego, E. M. and da Silva, A. L. P., ‘An optimal nonlinear extension of Banach–Stone theorem’, J. Funct. Anal. 271(8) (2016), 2166–2176.10.1016/j.jfa.2016.07.008CrossRefGoogle Scholar
Hess, H. U., ‘On a theorem of Cambern’, Proc. Amer. Math. Soc. 71(2) (1978), 204–206.10.1090/S0002-9939-1978-0500490-8CrossRefGoogle Scholar
Hirsberg, B., ‘Représentations intégrales des formes linéaires complexes’, C. R. Acad. Sci. Paris Sér. A-B 274 (1972), A1222–A1224.Google Scholar
Holický, P. and Spurný, J., ‘Perfect images of absolute Souslin and absolute Borel Tychonoff spaces’, Topol. Appl. 131(3) (2003), 281–294.10.1016/S0166-8641(02)00356-5CrossRefGoogle Scholar
Hustad, O., ‘A norm preserving complex Choquet theorem’, Math. Scand. 29 (1971), 272–278; (1972).10.7146/math.scand.a-11053CrossRefGoogle Scholar
Jarosz, K., ‘Into isomorphisms of spaces of continuous functions’, Proc. Amer. Math. Soc. 90(3) (1984), 373–377.10.1090/S0002-9939-1984-0728351-2CrossRefGoogle Scholar
Jarosz, K., Perturbations of Banach Algebras, Lecture Notes in Mathematics, 1120 (Springer, Berlin, 1985).10.1007/BFb0076885CrossRefGoogle Scholar
Jarosz, K., ‘Small isomorphisms of C (X, E) spaces’, Pac. J. Math. 138(2) (1989), 295–315.10.2140/pjm.1989.138.295CrossRefGoogle Scholar
Jarosz, K. and Pathak, V. D., ‘Isometries and small bound isomorphisms of function spaces’, in: Function Spaces (Edwardsville, IL, 1990), Lecture Notes in Pure and Applied Mathematics, 136 (Dekker, New York, 1992), 241–271.Google Scholar
Koumoullis, G., ‘A generalization of functions of the first class’, Topol. Appl. 50(3) (1993), 217–239.10.1016/0166-8641(93)90022-6CrossRefGoogle Scholar
Ludvík, P. and Spurný, J., ‘Isomorphisms of spaces of continuous affine functions on compact convex sets with Lindelöf boundaries’, Proc. Amer. Math. Soc. 139(3) (2011), 1099–1104.10.1090/S0002-9939-2010-10534-8CrossRefGoogle Scholar
Lukeš, J., Malý, J., Netuka, I. and Spurný, J., Integral Representation Theory, de Gruyter Studies in Mathematics, 35, Applications to Convexity, Banach Spaces and Potential Theory (Walter de Gruyter, Berlin, 2010).Google Scholar
Rondoš, J. and Spurný, J., ‘Isomorphisms of spaces of affine continuous complex functions’, Math. Scand. 125(2) (2019), 270–290.10.7146/math.scand.a-114989CrossRefGoogle Scholar
Roth, W., ‘Choquet theory for vector-valued functions on a locally compact space’, J. Convex Anal. 21(4) (2014), 1141–1164.Google Scholar
Saab, P. and Talagrand, M., ‘A Choquet theorem for general subspaces of vector-valued functions’, Math. Proc. Cambridge Philos. Soc. 98(2) (1985), 323–326.10.1017/S0305004100063490CrossRefGoogle Scholar
Spurný, J., ‘Borel sets and functions in topological spaces’, Acta Math. Hungar. 129(1–2) (2010), 47–69.10.1007/s10474-010-9223-6CrossRefGoogle Scholar