Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-28T06:12:39.605Z Has data issue: false hasContentIssue false
  • English
  • Français

SMOOTH VALUES OF POLYNOMIALS

Part of: General field theory Multiplicative number theory

Published online by Cambridge University Press:  01 February 2019

J. W. BOBER ,
D. FRETWELL ,
G. MARTIN  and
T. D. WOOLEY
J. W. BOBER*
Affiliation:
School of Mathematics, University of Bristol, University Walk, Clifton, Bristol BS8 1TW, UK The Heilbronn Institute for Mathematical Research, Bristol, UK email j.bober@bristol.ac.uk
D. FRETWELL
Affiliation:
School of Mathematics, University of Bristol, University Walk, Clifton, BristolBS8 1TW, UK The Heilbronn Institute for Mathematical Research, Bristol, UK email daniel.fretwell@bristol.ac.uk
G. MARTIN
Affiliation:
Department of Mathematics, University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver, BC, Canada V6T 1Z2 email gerg@math.ubc.ca
T. D. WOOLEY
Affiliation:
School of Mathematics, University of Bristol, University Walk, Clifton, Bristol BS8 1TW, UK email matdw@bristol.ac.uk
*
✉j.bober@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Given 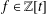$f\in \mathbb{Z}[t]$ of positive degree, we investigate the existence of auxiliary polynomials 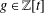$g\in \mathbb{Z}[t]$ for which 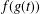$f(g(t))$ factors as a product of polynomials of small relative degree. One consequence of this work shows that for any quadratic polynomial 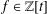$f\in \mathbb{Z}[t]$ and any 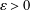$\unicode[STIX]{x1D700}>0$, there are infinitely many 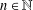$n\in \mathbb{N}$ for which the largest prime factor of 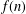$f(n)$ is no larger than 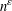$n^{\unicode[STIX]{x1D700}}$.

Keywords

Smooth numberspolynomialssmall degree irreducible factors

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Secondary: 11N25: Distribution of integers with specified multiplicative constraints 12E05: Polynomials (irreducibility, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 2 , April 2020 , pp. 245 - 261
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author’s work is partially supported by a National Sciences and Engineering Research Council of Canada Discovery Grant. The fourth author’s work is supported by a European Research Council Advanced Grant under the European Union’s Horizon 2020 research and innovation programme via grant agreement no. 695223.

References

Balog, A. and Wooley, T. D., ‘On strings of consecutive integers with no large prime factors’, J. Aust. Math. Soc. Ser. A 64(2) (1998), 266–276.Google Scholar
Bhargava, M., ‘Most hyperelliptic curves over $\mathbb{Q}$ have no rational points’, Preprint, 2013, available at arXiv:1308:0395.Google Scholar
Bhargava, M., Gross, B. H. and Wang, X., ‘A positive proportion of locally soluble hyperelliptic curves over ℚ have no point over any odd degree extension’ (with an appendix by T. Dokchitser and V. Dokchitser), J. Amer. Math. Soc. 30(2) (2017), 451–493.Google Scholar
Dartyge, C., Martin, G. and Tenenbaum, G., ‘Polynomial values free of large prime factors’, Period. Math. Hungar. 43(1–2) (2001), 111–119.Google Scholar
Granville, A. and Pleasants, P., ‘Aurifeuillian factorization’, Math. Comp. 75(253) (2006), 497–508.Google Scholar
Harrington, J., ‘On the factorization of the trinomials x n + cx n-1 + d’, Int. J. Number Theory 8(6) (2012), 1513–1518.Google Scholar
Ljunggren, W., ‘On the irreducibility of certain trinomials and quadrinomials’, Math. Scand. 8 (1960), 65–70.Google Scholar
Martin, G., ‘An asymptotic formula for the number of smooth values of a polynomial’, J. Number Theory 93(2) (2002), 108–182.Google Scholar
Schinzel, A., ‘On two theorems of Gelfond and some of their applications’, Acta Arith. 13 (1967), 177–236.Google Scholar
Schinzel, A., Polynomials with Special Regard to Reducibility, Encyclopedia of Mathematics and its Applications, 77 (Cambridge University Press, Cambridge, 2000).Google Scholar
Selmer, E. S., ‘On the irreducibility of certain trinomials’, Math. Scand. 4 (1956), 287–302.Google Scholar