Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T05:14:25.303Z Has data issue: false hasContentIssue false
  • English
  • Français

SUMS OF SQUARES AND PARTITION CONGRUENCES

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  18 March 2020

SU-PING CUI  and
NANCY S. S. GU Open the ORCID record for NANCY S. S. GU [Opens in a new window]
SU-PING CUI
Affiliation:
School of Mathematics and Statistics, Qinghai Normal University, Xining, Qinghai810008, PR China Academy of Plateau Science and Sustainability, Xining, Qinghai810008, PR China e-mail: jiayoucui@163.com
NANCY S. S. GU
Affiliation:
Center for Combinatorics, LPMC, Nankai University, Tianjin300071, PR China e-mail: gu@nankai.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

For positive integers $n$ and 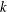$k$, let 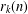$r_{k}(n)$ denote the number of representations of $n$ as a sum of 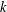$k$ squares, where representations with different orders and different signs are counted as distinct. For a given positive integer $m$, by means of some properties of binomial coefficients, we derive some infinite families of congruences for 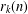$r_{k}(n)$ modulo 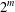$2^{m}$. Furthermore, in view of these arithmetic properties of 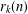$r_{k}(n)$, we establish many infinite families of congruences for the overpartition function and the overpartition pair function.

Keywords

sums of squarescongruencespartitionsoverpartitions

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 249 - 267
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Coons

This work was supported by the National Natural Science Foundation of China, the Fundamental Research Funds for the Central Universities of China, the Natural Science Foundation for Young Scientists of Qinghai Province and Outstanding Chinese, and the Foreign Youth Exchange Program of the China Association of Science and Technology.

References

Barrucand, P. and Hirschhorn, M. D., ‘Formulae associated with 5, 7, 9 and 11 squares’, Bull. Austral. Math. Soc. 65 (2002), 503–510.Google Scholar
Berndt, B. C., Dixit, A., Kim, S. and Zaharescu, A., ‘On a theorem of A. I. Popov on sums of squares’, Proc. Amer. Math. Soc. 145 (2017), 3795–3808.Google Scholar
Berndt, B. C., Dixit, A., Kim, S. and Zaharescu, A., ‘Sums of squares and products of Bessel functions’, Adv. Math. 338 (2018), 305–338.Google Scholar
Chen, W. Y. C., Hou, Q.-H., Sun, L. H. and Zhang, L., ‘Ramanujan-type congruences for overpartitions modulo 16’, Ramanujan J. 40 (2016), 311–322.Google Scholar
Chen, W. Y. C. and Lin, B. L. S., ‘Properties of overpartition pairs’, Acta Arith. 151 (2012), 263–277.Google Scholar
Chen, W. Y. C., Sun, L. H., Wang, R. H. and Zhang, L., ‘Ramanujan-type congruences for overpartitions modulo 5’, J. Number Theory 148 (2015), 62–72.Google Scholar
Chen, W. Y. C. and Xia, E. X. W., ‘Proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Acta Arith. 163 (2014), 59–69.Google Scholar
Cooper, S., ‘On sums of an even number of squares, and an even number of triangular numbers: an elementary approach based on Ramanujans 1𝜓1 summation formula’, in: q-Series with Applications to Combinatorics, Number Theory and Physics, Contemporary Mathematics, 291 (eds. Berndt, B. C. and Ono, K.) (American Mathematical Society, Providence, RI, 2001), 115–137.Google Scholar
Cooper, S., ‘Sums of five, seven and nine squares’, Ramanujan J. 6 (2002), 469–490.Google Scholar
Cooper, S., ‘On the number of representations of certain integers as sums of 11 or 13 squares’, J. Number Theory 103 (2003), 135–162.Google Scholar
Cooper, S. and Hirschhorn, M. D., ‘On the number of primitive representations of integers as sums of squares’, Ramanujan J. 13 (2007), 7–25.Google Scholar
Corteel, S. and Lovejoy, J., ‘Overpartitions’, Trans. Amer. Math. Soc. 356 (2004), 1623–1635.Google Scholar
Fortin, J.-F., Jacob, P. and Mathieu, P., ‘Jagged partitions’, Ramanujan J. 10 (2005), 215–235.Google Scholar
Gasper, G. and Rahman, M., Basic Hypergeometric Series, 2d edn (Cambridge University Press, Cambridge, 2004).Google Scholar
Glaisher, J. W. L., ‘On the numbers of representations of a number as a sum of 2r squares, where 2r does not exceed eighteen’, Proc. Lond. Math. Soc. 5 (1907), 479–490.Google Scholar
Hardy, G. H., ‘On the representation of a number as the sum of any number of squares, and in particular of five or seven’, Proc. Natl Acad. Sci. USA 4 (1918), 189–193.Google Scholar
Hardy, G. H., ‘On the representation of a number as the sum of any number of squares, and in particular of five’, Trans. Amer. Math. Soc. 21 (1920), 255–284.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘On representations of a number as a sum of three squares’, Discrete Math. 199 (1999), 85–101.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic relations for overpartitions’, J. Combin. Math. Combin. Comput. 53 (2005), 65–73.Google Scholar
Jacobi, C. G. J., Fundamenta Nova Theoriae Functionum Ellipticarum (1829), (reprinted in Gesammelte Werke, vol. 1, Berlin, 1881, 49–239; see pp. 159, 160, 164, 170. Reprinted by Chelsea, New York, 1969).Google Scholar
Kim, B., ‘A short note on the overpartition function’, Discrete Math. 309 (2009), 2528–2532.Google Scholar
Lin, B. L. S., ‘A new proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Ramanujan J. 38 (2015), 199–209.Google Scholar
Lomadze, G. A., ‘On the number of representations of natural numbers by sums of nine squares’, Acta Arith. 68 (1994), 245–253.Google Scholar
Lovejoy, J., ‘Gordon’s theorem for overpartitions’, J. Combin. Theory Ser. A 103 (2003), 393–401.Google Scholar
Mahlburg, K., ‘The overpartition function modulo small powers of 2’, Discrete Math. 286 (2004), 263–267.Google Scholar
Mordell, L. J., ‘On the representation of numbers as the sum of 2r squares’, Q. J. Pure Appl. Math. 48 (1917), 93–104.Google Scholar
Newman, M., ‘Subgroups of the modular group and sums of squares’, Amer. J. Math. 82 (1960), 761–778.Google Scholar
Ramanujan, S., ‘On certain arithmetical functions’, Trans. Cambridge Philos. Soc. 22 (1916), 159–184; (reprinted in Collected Papers of Srinivasa Ramanujan, AMS Chelsea, Providence, RI, 2000, 136–162).Google Scholar
Sandham, H. F., ‘A square as the sum of 7 squares’, Quart. J. Math. 4 (1953), 230–236.Google Scholar
Sandham, H. F., ‘A square as the sum of 9, 11 and 13 squares’, J. Lond. Math. Soc. 29 (1954), 31–38.Google Scholar
Xiong, X., ‘Overpartitions and ternary quadratic forms’, Ramanujan J. 42 (2017), 429–442.Google Scholar
Yao, O. X. M. and Xia, E. X. W., ‘New Ramanujan-like congruences modulo powers of 2 and 3 for overpartitions’, J. Number Theory 133 (2013), 1932–1949.Google Scholar