Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T12:18:20.319Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES

Part of: Diophantine approximation, transcendental number theory Differential and difference algebra Sequences and sets

Published online by Cambridge University Press:  11 November 2014

PETER BUNDSCHUH  and
KEIJO VÄÄNÄNEN
PETER BUNDSCHUH*
Affiliation:
Mathematisches Institut, Universität zu Köln, Weyertal 86-90, 50931 Köln, Germany email pb@math.uni-koeln.de
KEIJO VÄÄNÄNEN
Affiliation:
Department of Mathematical Sciences, University of Oulu, PO Box 3000, 90014 Oulun Yliopisto, Finland email keijo.vaananen@oulu.fi
*
✉pb@math.uni-koeln.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper considers algebraic independence and hypertranscendence of functions satisfying Mahler-type functional equations $af(z^{r})=f(z)+R(z)$, where $a$ is a nonzero complex number, $r$ an integer greater than 1, and 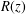$R(z)$ a rational function. Well-known results from the scope of Mahler’s method then imply algebraic independence over the rationals of the values of these functions at algebraic points. As an application, algebraic independence results on reciprocal sums of Fibonacci and Lucas numbers are obtained.

Keywords

algebraic independence of functionsalgebraic independence of numbershypertranscendenceMahler’s methodreciprocal sums of Fibonacci and Lucas numbers

MSC classification

Primary: 11J91: Transcendence theory of other special functions
Secondary: 11J81: Transcendence (general theory) 11B39: Fibonacci and Lucas numbers and polynomials and generalizations 12H05: Differential algebra 39B32: Equations for complex functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 289 - 310
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Bundschuh, P., ‘Transcendence and algebraic independence of series related to Stern’s sequence’, Int. J. Number Theory 8 (2012), 361–376.Google Scholar
Coons, M., ‘Extension of some theorems of W. Schwarz’, Canad. Math. Bull. 55 (2012), 60–66.CrossRefGoogle Scholar
Duverney, D., Kanoko, T. and Tanaka, T., ‘Transcendence of certain reciprocal sums of linear recurrences’, Monatsh. Math. 137 (2002), 115–128.CrossRefGoogle Scholar
Duverney, D. and Nishioka, Ku., ‘An inductive method for proving transcendence of certain series’, Acta Arith. 110 (2003), 305–330.CrossRefGoogle Scholar
Hilbert, D., ‘Mathematical problems’, Bull. Amer. Math. Soc. 8 (1902), 437–479; transl. from: ‘Mathematische Probleme’, Nachr. Königl. Ges. Wiss Göttingen Math.-Phys. Kl. Heft 3 (1900), 253–297.Google Scholar
Kanoko, T., Kurosawa, T. and Shiokawa, I., ‘Transcendence of reciprocal sums of binary recurrences’, Monatsh. Math. 157 (2009), 323–334.Google Scholar
Kurosawa, T., ‘Transcendence of certain series involving binary linear recurrences’, J. Number Theory 123 (2007), 35–58.CrossRefGoogle Scholar
Loxton, J. H. and van der Poorten, A. J., ‘A class of hypertranscendental functions’, Aequationes Math. 16 (1977), 93–106.Google Scholar
Mahler, K., ‘Arithmetische Eigenschaften einer Klasse transzendental-transzendenter Funktionen’, Math. Z. 32 (1930), 545–585.CrossRefGoogle Scholar
Mahler, K., ‘Remarks on a paper by W. Schwarz’, J. Number Theory 1 (1969), 512–521.Google Scholar
Nishioka, Ke., ‘A note on differentially algebraic solutions of first order linear difference equations’, Aequationes Math. 27 (1984), 32–48.Google Scholar
Nishioka, Ke., ‘Algebraic function solutions of a certain class of functional equations’, Arch. Math. (Basel) 44 (1985), 330–335.CrossRefGoogle Scholar
Nishioka, Ku., Mahler Functions and Transcendence, Lecture Notes in Mathematics, 1631 (Springer, Berlin, 1996).Google Scholar
Nishioka, Ku., ‘Algebraic independence of reciprocal sums of binary recurrences’, Monatsh. Math. 123 (1997), 135–148.Google Scholar
Nishioka, Ku., ‘Algebraic independence of reciprocal sums of binary recurrences II’, Monatsh. Math. 136 (2002), 123–141.Google Scholar
Nishioka, Ku., Tanaka, T. and Toshimitsu, T., ‘Algebraic independence of sums of reciprocals of the Fibonacci numbers’, Math. Nachr. 202 (1999), 97–108.CrossRefGoogle Scholar
Tanaka, T., ‘Algebraic independence results related to linear recurrences’, Osaka J. Math. 36 (1999), 203–227.Google Scholar
Toshimitsu, T., ‘ q-additive functions and algebraic independence’, Arch. Math. (Basel) 69 (1997), 112–119.CrossRefGoogle Scholar