Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:01:50.116Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ARITHMETICAL EXCURSION VIA STONEHAM NUMBERS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  27 March 2014

MICHAEL COONS
MICHAEL COONS*
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, University Drive, Callaghan NSW 2308, Australia email mcoons.newcastle@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 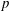$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ be a prime and 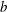$b$ a primitive root of 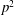$p^2$. In this paper, we give an explicit formula for the number of times a value in 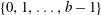$\{0,1,\ldots,b-1\}$ occurs in the periodic part of the base-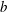$b$ expansion of 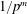$1/p^m$. As a consequence of this result, we prove two recent conjectures of Aragón Artacho et al. [‘Walking on real numbers’, Math. Intelligencer35(1) (2013), 42–60] concerning the base-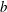$b$ expansion of Stoneham numbers.

Keywords

Stoneham numbersbase-b expansionsnormal numbers

MSC classification

Secondary: 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 3 , June 2014 , pp. 303 - 315
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aragón Artacho, F. J., Bailey, D. H., Borwein, J. M. and Borwein, P. B., ‘Walking on real numbers’, Math. Intelligencer 35(1) (2013), 42–60.Google Scholar
Bailey, D. H. and Borwein, J. M., ‘Normal numbers and pseudorandom generators’, in: Proceedings of the Workshop on Computational and Analytical Mathematics in Honour of Jonathan Borwein’s 60th Birthday (Springer, New York, 2013).Google Scholar
Bailey, David H. and Crandall, Richard E., ‘Random generators and normal numbers’, Experiment. Math. 11(4) (2003), 527–546.Google Scholar
Bailey, David H. and Misiurewicz, Michał, ‘A strong hot spot theorem’, Proc. Amer. Math. Soc. 134(9) (2006), 2495–2501.Google Scholar
Champernowne, D. G., ‘The construction of decimals normal in the scale of ten’, J. Lond. Math. Soc. 8(4) (1933), 254.CrossRefGoogle Scholar
Nishioka, Keiji, ‘Algebraic function solutions of a certain class of functional equations’, Arch. Math. 44 (1985), 330–335.Google Scholar
Nishioka, Kumiko, Mahler Functions and Transcendence, Lecture Notes in Mathematics, 1631 (Springer, Berlin, 1996).Google Scholar
Mahler, Kurt, ‘Arithmetische Eigenschaften der Lösungen einer Klasse von Funktionalgleichungen’, Math. Ann. 101(1) (1929), 342–366.Google Scholar
Mahler, Kurt, ‘Arithmetische Eigenschaften einer Klasse von Dezimalbrüchen’, Proc. Kon. Nederlandsche Akad. v. Wetenschappen 40 (1937), 421–428.Google Scholar
Rosen, Kenneth H., Elementary Number Theory and Its Applications. 5th edn (Addison-Wesley, Reading, MA, 2005).Google Scholar
Schmidt, Wolfgang M., ‘On normal numbers’, Pacific J. Math. 10 (1960), 661–672.Google Scholar
Stoneham, R. G., ‘On absolute (j, ε)-normality in the rational fractions with applications to normal numbers’, Acta Arith. 22 (1972/73), 277–286.Google Scholar