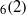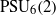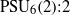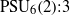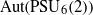Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Parker, Chris
and
Stroth, Gernot
2014.
and its automorphism group.
Journal of Pure and Applied Algebra,
Vol. 218,
Issue. 5,
p.
852.
Oliver, Bob
2022.
Fusion systems realizing certain Todd modules.
Journal of Group Theory,
Vol. 0,
Issue. 0,
Parker, Chris
Pientka, Gerald
Seidel, Andreas
and
Stroth, Gernot
2023.
Finite Groups Which are Almost Groups of Lie Type in Characteristic 𝐩.
Memoirs of the American Mathematical Society,
Vol. 292,
Issue. 1452,