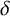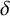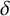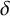AN INCIDENCE RESULT FOR WELL-SPACED ATOMS IN ALL DIMENSIONS

Abstract

We prove an incidence result counting the k-rich $\delta $-tubes induced by a well-spaced set of $\delta $-atoms. Our result coincides with the bound that would be heuristically predicted by the Szemerédi–Trotter theorem and holds in all dimensions $d \geq 2$. We also prove an analogue of Beck’s theorem for $\delta $-atoms and $\delta $-tubes as an application of our result.

1 Introduction

Incidence geometry is concerned with counting incidences between various geometric objects, traditionally points and lines. Given a finite set of lines L in $\mathbb {R}^2$ , a point is k-rich if between k and $2k$ lines from L pass through it. The set of k-rich points is denoted by $P_k(L)$ . For $k\geq 2$ , the classical Szemerédi–Trotter theorem [13] bounds sharply $|P_k(L)|$ :

(1-1) $$ \begin{align} |P_k(L)| \lesssim |L|^2 k^{-3} + |L| k^{-1}. \end{align} $$

By duality, the above bound also holds if the roles of points and lines are interchanged. If $L_k(P)$ is the set of k-rich lines induced by a set P of points, then

(1-2) $$ \begin{align} |L_k(P)| \lesssim |P|^2 k^{-3} + |P| k^{-1}. \end{align} $$

Given a set P of points and a set L of lines in $\mathbb {R}^2$ , the number of incidences is defined to be $\mathcal {I}(P,L) := |\{(p,l) \in P\times L: p\in l\}|$ . An equivalent formulation of the Szemerédi–Trotter Theorem states that

(1-3) $$ \begin{align} \mathcal{I}(P,L) \lesssim (|P||L|)^{2/3} + |P| + |L|. \end{align} $$

In their 2019 paper [11], Guth et al. proved an analogue of the Szemerédi–Trotter theorem akin to Equation (1-1), for suitably well-spaced sets of tubes of thickness $\delta $ in $[0,1]^2$ . Furthermore, they proved a similar result in $[0,1]^3$ which is an analogue of the seminal Guth–Katz bound [9]. Both bounds are essentially sharp. Their work expands our understanding of the Kakeya problem which studies intersections of thin tubes.

As in [11], our objects of interest are small $\delta $ -atoms and thin $\delta $ -tubes. A $\delta $ -atom is a closed ball in $[0,1]^d$ of diameter $\delta $ and a $\delta $ -tube is the set of all points in $[0,1]^d$ which are within a distance $\delta /2$ of some fixed line. Throughout this paper, distance will always refer to Euclidean distance. Unlike the discrete setting of points and lines, we need to carefully define what it means for two atoms or two tubes to be distinct. Two $\delta $ -atoms are distinct if they do not intersect each other. Two $\delta $ -tubes are distinct if either:

• • they do not intersect each other; or

• • the angle between them is greater than $\delta $ .

Unless otherwise stated, atoms and tubes will be assumed throughout to be distinct.

In the literature, these criteria are often summarised by saying that a set A of atoms or a set T of tubes is $\delta $ -separated. (Technically, they are $2\delta $ -separated under the forthcoming definition.) More generally, we can state the following definition.

Definition 1.1. Given $\gamma \geq \delta $ , we say a set of $\delta $ -atoms A (respectively $\delta $ -tubes T) are $\gamma $ -separated if there is at most one atom of A (respectively tube of T) in each $\gamma $ -atom (respectively $\gamma $ -tube).

We say that an atom and a tube are incident with each other if they have a nonempty intersection. If the number of atoms from A incident with a $\delta $ -tube lies in $[k,2k)$ , then we say it is a k-rich tube (induced by A). Let $T_k(A)$ be the set of k-rich $\delta $ -tubes induced by A. Owing to the above setup, a set of atoms A must always be finite.

The problem we address is upper-bounding $|T_k(A)|$ . In two dimensions, this problem is dual to one of the aforementioned problems addressed in [11]. Bounding the number of incidences between a set A of atoms and a set T of tubes is an equivalent way of studying this problem.

An alternative setup involves counting approximate incidences between $\delta $ -separated points and $\delta $ -separated lines. In this setting, we would say that a point p and a line l are incident if p lies in a $\delta $ -neighbourhood of the line l. This is the setup used in [4].

Defining distinct atoms and distinct tubes in the above way is natural because it avoids degenerate configurations of atoms and tubes. To give an example, let us allow atoms to intersect. Let A be a large set of atoms that are all small perturbations of a single atom, and let T be a large set of tubes arranged in a star shape and all passing through the atoms of A. In this configuration, all atoms are incident with all tubes, which ought not to happen in a good setup of a continuous incidence problem. Indeed, the correct interpretation for two atoms which intersect each other is that they are two copies of the same atom. We would say that this atom appears with multiplicity two. In Section 2, we give an incidence result in which the atoms in A may appear with multiplicity.

However, even with these assumptions, atoms and tubes are still not a perfect model for points and lines. In discrete geometry, two points can lie on at most one line and two lines can intersect in at most one point. However, this does not hold for atoms and tubes, and constitutes one of the most important differences between the two cases. In fact, if two $\delta $ -atoms in $[0,1]^d$ are separated by a distance of x where $\delta \lesssim x < 1$ , then there exist $\sim x^{1-d}$ distinct $\delta $ -tubes that are incident to both of them.

The following example illustrates that without further assumptions on the distribution of atoms, bounds that match the Szemerédi–Trotter theorem in Equation (1-2) are unobtainable.

Example 1.2. Suppose A is a grid of $\delta $ -atoms with $|A| = k^2 $ , that fit inside some $k\delta \times k\delta $ square in $[0,1]^2 $ . It is clear that $|T_k(A)| \sim k\delta ^{-1} = \delta ^{-1}\cdot {|A|^2}/{k^3}$ . Since $\delta ^{-1}$ can be arbitrarily large, any upper bounds on $|T_k(A)|$ will be very weak. Similar problematic examples can also be constructed in higher dimensions.

The following incidence bound is the dual to a result established in [4].

Theorem 1.3 (Fässler, Orponen, Pinamonti).

Let A be a set of $W^{-1}$ -separated $\delta $ -atoms in $[0,1]^2$ where $1< W \leq \delta ^{-1}$ . Let $T_k(A)$ be the set of k-rich $\delta $ -tubes induced by A. Then

$$ \begin{align*} |T_k(A)| \lesssim W\cdot \frac{|A|^2}{k^3}. \end{align*} $$

In light of Example 1.2, Theorem 1.3 is sharp when $W = \delta ^{-1}$ . However, when $k\leq \delta |A|$ , this bound is worse than the trivial $|T_k(A)| \lesssim \delta ^{-2}$ and indeed there exist sets A of atoms which attain this trivial bound.

For a set A of $\delta $ -atoms in $[0,1]^d$ that is well distributed in some sense, we prove a bound for $|T_k(A)|$ which essentially depends only on $|A|$ and k. In this context, well distributed means that the atoms almost form a well-spaced grid.

Theorem 1.4. Let $d\geq 2$ be an integer. Given $1<W<\delta ^{-1}$ , let A be a $W^{-1}$ -separated family of $\delta $ -atoms in $[0,1]^d$ where $|A| \sim W^{d}$ . Let $k \geq 2$ . Then for every $\epsilon> 0$ , there exist $C_1(\epsilon ,d)$ and $C_2(\epsilon ,d)$ such that if

(1-4) $$ \begin{align} k\geq C_1(\epsilon, d)\delta^{-\epsilon}\cdot \delta^{d-1}|A|, \end{align} $$

then

(1-5) $$ \begin{align} |T_k(A)| \leq C_2(\epsilon,d) \delta^{-\epsilon} \cdot \frac{|A|^2}{k^3}. \end{align} $$

Remark 1.5. Let $T_{\geq k}(A)$ be the set of at least k-rich tubes induced by A. After dyadic summing, it is clear that Theorem 1.4 obtains the same asymptotic bounds for $|T_{\geq k}(A)|$ and $|T_k(A)|$ . In the literature, there is usually no distinction made between these quantities.

The condition in Equation (1-4) on k is necessary and has a specific meaning. If the atoms in A were randomly placed, then a simple calculation verifies that the expected richness of any $\delta $ -tube is $\delta ^{d-1}|A|$ . If $k\leq \delta ^{d-1}|A|$ , then probabilistic arguments prove that there exist configurations of atoms A such that a positive proportion of all possible $\delta $ -tubes are at least k-rich. Thus we need Equation (1-4) to obtain nontrivial bounds for $|T_k(A)|$ .

Compared to Theorem 1.3, our Theorem 1.4 has the key added assumption that $|A| = W^d$ , which means that A is as big as a $W^{-1}$ -separated set could be. In other words, A nearly forms a grid of atoms. In contrast, Theorem 1.3 applies to much sparser sets of atoms that are still $W^{-1}$ -separated.

Given a general set T of tubes, $\mathcal {I}(A,T)$ will be the number of incidences between atoms from A and tubes from T. Concretely,

$$ \begin{align*}\mathcal{I}(A,T) := |\{(a,t)\in A \times T: a\cap t \neq \emptyset\}|.\end{align*} $$

We can obtain an equivalent formulation of Theorem 1.4 in terms of incidences by a standard argument.

Corollary 1.6. Let $d\geq 2$ be an integer. Given $1<W<\delta ^{-1}$ , let A be a $W^{-1}$ -separated family of $\delta $ -atoms in $[0,1]^d$ where $|A| \sim W^{d}$ . Let T be an arbitrary set of distinct $\delta $ -tubes. Then for every $\epsilon> 0$ , there exists $C_3(\epsilon ,d)$ , such that

(1-6) $$ \begin{align} \mathcal{I}(A,T) \leq C_3(\epsilon,d) \delta^{-\epsilon}(|A|^{2/3}|T|^{2/3} + k_0(A,\delta)|T|), \end{align} $$

where $k_0(A,\delta ) := \max \{1,\delta ^{d-1}|A|\}$ .

The term $k_0(A,\delta )|T|$ in Equation (1-6) plays the same role as the $|L|$ term in the Szemerédi–Trotter bound Equation (1-3), namely counting the incidences from lines incident to only one point.

Let us now briefly clarify how our contribution fits in with the results from [11] upon which our methods are inspired. The main result proved in [11] bounds the number $|A_k(T)|$ of k-rich atoms induced by a set T of well-distributed tubes.

Theorem 1.7 (Guth–Solomon–Wang).

Let $d=2$ or $3$ . Given $1<W<\delta ^{-1}$ , let T be a $W^{-1}$ -separated family of $\delta $ -tubes in $[0,1]^d$ where $|A| \sim W^{2(d-1)}$ . Let $k \geq 2$ . Then for every $\epsilon> 0$ , there exist $C_1(\epsilon ,d)$ and $C_2(\epsilon ,d)$ such that if

$$\begin{align*} k\geq C_1(\epsilon, d)\delta^{-\epsilon}\cdot \delta^{d-1}|T|, \end{align*}$$

then

$$\begin{align*} |A_k(T)| \leq C_2(\epsilon,d) \delta^{-\epsilon} \cdot \frac{|T|^{{d}/({d-1})}}{k^{({d+1})/({d-1})}}. \end{align*}$$

We say a set A of atoms is well distributed if it satisfies the conditions in Theorem 1.4. Similarly, we say a set T of tubes is well distributed if it satisfies the conditions in Theorem 1.7. In dimension $d=2$ , well-distributed atoms and tubes are dual to each other. Lines in two dimensions are parametrised by two variables, so a set of well-distributed $\delta $ -tubes becomes a set of well-distributed $\delta $ -atoms when viewed in the parameter space. Thus, the $d=2$ case of Theorem 1.4 follows immediately by duality from Theorem 1.7. This result is essentially optimal.

However, for all $d\geq 3$ , Theorem 1.4 is a new result. It cannot be obtained by reparametrising Theorem 1.7 or any other existing result. When $d\geq 3$ , we conjecture that the bound should have $k^3$ replaced with $k^{d+1}$ in the denominator of Equation (1-5), but any improvement towards this appears not to be amenable to the method we use. The obstacles to obtaining stronger results for $d\geq 3$ appear to be related to the reasons that the method in [11] fails if $d>3$ . In both cases, proving a suitable modification of Proposition 2.1 (and its analogue from [11]) would yield improvements.

A discrete version of Theorem 1.4 can be obtained in any dimension $d\geq 3$ by projecting generically onto a plane and applying the Szemerédi–Trotter theorem. However, this is not possible in the thickened setting because projecting into a plane will not preserve the well-distributed property of the set of atoms in general.

Remark 1.8. It does not matter if we define our atoms to be $\delta $ -balls with respect to the $\| \cdot \|_2$ norm or the $\| \cdot \|_\infty $ norm, that is, whether our atoms are d-dimensional balls or cubes. It only matters that there exist constants $C,c$ such that a $\delta $ -cube is always contained in a $C\delta $ -ball, and also contains a $c\delta $ -ball. The choice of shape then only affects multiplicative constants in our bounds, which are of no consequence since we are primarily interested in growth rate. During our proof, we partition the space $[0,1]^d$ into ‘cells’, which is most natural if we view our cells as smaller d-dimensional cubes. One important upshot is that all equalities in this paper are implicitly up to absolute constants. None of these constants are problematically large or small.

Several other recent atom–tube incidence bounds with different spacing conditions are worth noting. Fu et al. [5] proved a generalisation of Theorem 1.7 with the following more permissive spacing assumption: for $1 \leq W \leq X \leq \delta ^{-1}$ , T is a set of $X^{-1}$ -separated tubes with at most $X/W$ tubes in each $1 \times W^{-1}$ rectangle. Indeed, their result recovers the $d=2$ case of Theorem 1.7 when $X = W$ . Fu and Ren [6] also addressed incidence estimations where the set of atoms (respectively tubes) behave locally like $\alpha $ -dimensional (respectively $\beta $ -dimensional) sets for fixed $\alpha , \beta $ .

Our focus in this paper is combinatorial, but it ought to be mentioned that studying the intersections of atoms and tubes is relevant to other problems in real analysis. A discretised version of the Erdős distinct distance problem is treated in [11] and the related Falconer distance conjecture has admitted recent improvements in the plane in [8].

Incidence geometry has been used for addressing sum-product type problems since the groundbreaking paper of Elekes [3]. A $\delta $ -discretised sum-product theorem was proved by Bourgain [2], and then reproved with explicit bounds by Guth et al. [10]. In recent work by Gan and Harbuzova [7], Elekes’ incidence geometry method was adapted to a version of the $\delta $ -discretised sum-product theorem with more restrictive assumptions on the set A. The more general discretised sum-product theorem appears impervious to being improved using continuous incidence geometry.

The structure of this paper is as follows: in Section 2, we prove a general incidence result which will be needed in the proof of Theorem 1.4 in Section 3. In Section 4, we give an application of Theorem 1.4, an analogue of Beck’s theorem for atoms and tubes.

Notation 1.9. We use asymptotic notation extensively. We write $f(n) \lesssim g(n)$ to mean that there exists a (positive) constant C such that $f(n) \leq Cg(n)$ for large n. We define $\lesssim _{\alpha , \beta }$ similarly, but in this case, the constant $C := C(\alpha ,\beta )$ may depend on $\alpha $ and $\beta $ .

2 A general incidence result

To assist in our proofs, we are mostly working with incidence counts rather than directly with k-rich tubes. Furthermore, we allow for sets of weighted atoms and tubes. Let A be a set of atoms where each $a\in A$ has a positive integer weight $w(a)$ associated with it. This essentially means that when counting incidences, the atom a appears $w(a)$ times. Similarly, we define the weight for sets of tubes.

For a set of weighted atoms A with weight function w, and a set of weighted tubes T with weight function $\omega $ , we define a more general incidence counting function

The following incidence bound is a generalisation of [11, Proposition 2.1] and our proof is a modification of theirs. Its uses for us are twofold. First, our proof of Theorem 1.4 requires an incidence result for a general set of atoms which may not be well distributed. Second, since it applies to weighted atoms, we can sidestep some technical steps in proving the main result.

The substance of Proposition 2.1 below is how the incidence count $\mathcal {I}(A,T)$ behaves when the atoms in A and the tubes in T are thickened by a factor of S. That is, each $\delta $ -atom becomes an $S\delta $ -atom centred at the same point, and each $\delta $ -tube becomes an $S\delta $ -tube about the same line. Importantly, after thickening, some atoms may intersect, in which case we consider them a single atom with an associated weight. If the original atoms were already weighted, then their weights sum if they intersect after thickening. Similarly, tubes may also become weighted after thickening.

Proposition 2.1. Fix $0 < \alpha < 1$ . Let $k \geq 1$ and A be a set of distinct weighted $\delta $ -atoms in $[0,1]^d$ with weight function w. Let T be a set of distinct (not weighted) $\delta $ -tubes. Let S be such that $\delta ^{-\alpha } \lesssim S \lesssim \delta ^{-1}$ . Then

(2-1) $$ \begin{align} \mathcal{I}(A,T) \lesssim \bigg(S\delta^{-(d-1)}|T|\sum_{a\in A}w(a)^2\bigg)^{1/2} + \delta^{-\alpha} S^{1-d}\mathcal{I}(A^S,T^S), \end{align} $$

where $A^S$ and $T^S$ are, respectively, the weighted sets of atoms and tubes formed by thickening A and T by a factor of S.

The proof of Proposition 2.1 uses some elementary Fourier analysis. We include the following definition for completeness.

Definition 2.2. For an integrable function $f: \mathbb {R}^d \rightarrow \mathbb {C}$ , its Fourier transform is defined as

$$ \begin{align*} \hat{f}(\xi) := \int_{\mathbb{R}^d} f(x) e^{-2\pi i x \cdot \xi}\, dx. \end{align*} $$

For two integrable functions $f: \mathbb {R}^d \rightarrow \mathbb {C}$ and $g: \mathbb {R}^d \rightarrow \mathbb {C}$ , their convolution is given by

$$ \begin{align*} (f\ast g)(x) := \int_{\mathbb{R}^d} f(y) g(x-y) \,dy. \end{align*} $$

Proof of Proposition 2.1.

We scale the problem by $\delta ^{-1}$ , so that the $\delta $ -atoms are now $1$ -atoms and the $\delta $ -tubes are now $1$ -tubes in $[0,\delta ^{-1}]^d$ . This will be more convenient to work with.

For any $a \in A$ and any $t\in T$ , let $\chi _a(x)$ and $\chi _t(x)$ , respectively, be smooth bump functions approximating the indicator functions for the atom a and the tube t. Now let $f(x) := \sum _{a\in A} w(a)\chi _a(x)$ and $g(x) := \sum _{t\in T} \chi _t(x)$ . In this notation,

$$ \begin{align*}\mathcal{I}(A,T) \sim \int_{[0,\delta^{-1}]^d} f(x)g(x)\,dx. \end{align*} $$

Since f and g are Lebesgue integrable functions, their Fourier transforms are well defined. Furthermore, since they are all bounded and supported on compact sets, they are $L_p$ functions for all p. It follows that Plancherel’s theorem holds: $\int f(x)g(x)\,dx = \int \hat {f}(\xi )\overline {\hat {g}(\xi )}\,d\xi $ . Decompose the above into high and low frequency parts:

$$ \begin{align*} \mathcal{I}(A,T) \sim \int \hat{f} \, \overline{\hat{g}}\, \eta + \int \hat{f} \, \overline{\hat{g}} \, (1-\eta), \end{align*} $$

where $\eta $ is a smooth function taking value $1$ on the ball of radius $\rho := \delta ^{-\alpha /d}S^{-1}$ and supported on a ball of radius $2\rho $ .

Low frequency case: Assume $\mathcal {I}(A,T) \lesssim \int \hat {f}\,\overline {\hat {g}}\, \eta $ . By Plancherel (and using that $\eta ^2 \approx \eta $ ),

$$ \begin{align*} \mathcal{I}(A,T) \lesssim \int (\,f \ast h) (g \ast h), \end{align*} $$

where $\overline {\hat {h}} = \eta $ . Roughly speaking, convolution with h thickens atoms and tubes by a factor of $\rho ^{-1}$ . For each atom $a \in A$ , the function $\chi _a \ast h$ is approximately $w(a) \rho ^d$ on the thickened $\rho ^{-1}$ -atom around a. Similarly, for each tube $t \in T$ , the function $\chi _t \ast h$ is approximately $\rho ^{d-1}$ on the thickened $\rho ^{-1}$ -tube around t.

Outside of these $\rho ^{-1}$ -atoms and $\rho ^{-1}$ -tubes, the functions $f\ast h$ and $g\ast h$ are rapidly decaying. Since $S = \delta ^{-\alpha /d} \rho ^{-1}$ , the tails of both functions are negligible outside the S-atoms $A^S$ and S-tubes $T^S$ . It follows that

$$ \begin{align*}\mathcal{I}(A,T) \lesssim \int (\,f \ast h) (g \ast h) \lesssim \rho^{d-1} \mathcal{I}(A^S,T^S) \lesssim \delta^{-\alpha} S^{1-d} \mathcal{I}(A^S,T^S). \end{align*} $$

High frequency case: Assume that $\mathcal {I}(A,T) \lesssim \int \hat {f}\,\overline {\hat {g}}\, (1-\eta )$ . Using the Cauchy–Schwarz inequality,

(2-2) $$ \begin{align} \int \hat{f}(\xi)\overline{\hat{g}(\xi)} (1-\eta(\xi))\,d\xi \leq \bigg(\int |\hat{f}(\xi)|^2 \,d\xi\bigg)^{1/2} \bigg(\int |\hat{g}(\xi)|^2 (1-\eta(\xi))^2 \,d\xi\bigg)^{1/2}. \end{align} $$

By Parseval’s identity, the first term on the right-hand side can be evaluated as

$$ \begin{align*}\bigg(\int |\hat{f}(\xi)|^2 \,d\xi\bigg)^{1/2} = \bigg(\int |f(x)|^2 \,dx\bigg)^{1/2} \sim \bigg(\sum_{a\in A} w(a)^2\bigg)^{1/2}.\end{align*} $$

We now estimate the second term on the right-hand side of Equation (2-2). Cover the d-dimensional unit sphere $S^{d-1} := \{ x \in \mathbb {R}^d : \|x\| = 1 \}$ with small $(d-1)$ -dimensional $\delta $ -balls. These will be called $\delta $ -caps and are used to sort tubes in T by direction. Let $T_\theta $ be the set of all tubes from T in the direction of $\delta $ -cap $\theta $ , and let $g_\theta = \sum _{t \in T_\theta } \chi _t$ . Then we need to estimate

$$ \begin{align*} \int |\hat{g}(\xi)|^2 (1-\eta(\xi))^2 \,d\xi = \int \bigg|\sum_\theta \hat{g_\theta}(\xi)\bigg|^2 (1-\eta(\xi))^2 \,d\xi. \end{align*} $$

We apply Cauchy–Schwarz to the sum over $\theta $ . The advantage is that for fixed $\xi $ , there are not many values of $\theta $ for which $\hat {g_\theta }(\xi )$ is nonzero.

For each $t \in T_\theta $ , we have that $\hat {\chi _t}$ is mostly supported on a $1\times \cdots \times 1 \times \delta $ slab orthogonal to $\theta $ and decays quickly outside. We call this slab $\theta ^\perp $ . Due to the rapidly decaying tails, the contribution of $\hat {g_\theta }$ outside the dilated slab $\delta ^{-\alpha /d}\theta ^\perp $ is of the order $\delta ^{B}$ for some positive B, and is therefore negligible.

Thus, the term $\hat {g_\theta }(\xi )$ is only nonzero if $\xi $ belongs to $\delta ^{-\alpha /d} \theta ^\perp $ . We may assume that $|\xi | \geq \rho $ , as $1-\eta (\xi )$ is otherwise zero. For such a large $\xi $ , simple geometric arguments show that $\xi $ belongs to $\delta ^{-\alpha /d} \theta ^\perp $ for at most $\lesssim \delta ^{-\alpha /d} \rho ^{-1} \delta ^{-(d-2)} = S\delta ^{-(d-2)}$ different $\theta $ values. Then Cauchy–Schwarz yields

$$ \begin{align*} (1-\eta(\xi))^2\bigg|\sum_\theta \hat{g_\theta}(\xi)\bigg|^2 \lesssim S\delta^{-(d-1)} \sum_{\theta} |\hat{g_\theta}(\xi)|^2.\end{align*} $$

Again using Parseval’s identity, it follows that

$$ \begin{align*}&\int |\hat{g}(\xi)|^2 (1-\eta(\xi))^2 \,d\xi \lesssim S\delta^{-(d-2)} \sum_\theta \int |\hat{g_\theta}(\xi)|^2 \,d\xi\\ &\quad= S\delta^{-(d-2)} \sum_\theta \int |g_\theta(x)|^2 \,dx = S\delta^{-(d-1)}|T|.\end{align*} $$

Substituting into Equation (2-2) yields

$$ \begin{align*}\mathcal{I}(A,T) \lesssim \bigg(S\delta^{-(d-1)}|T|\sum_{a\in A}w(a)^2\bigg)^{1/2}. \end{align*} $$

The dominant term in Equation (2-1) is determined based on whether the incidence count increases disproportionately after thickening by S. The following two examples give configurations of atoms and tubes that attain both bounds in Proposition 2.1, demonstrating that it is sharp up to a factor of S. For the purpose of these examples, A will not be a weighted set of atoms.

Example 2.3. If $A \subset [0,1]^d$ consists of all the $\delta $ -atoms in a d-dimensional box with side length $k\delta $ , then $|A| \sim k^d$ . If T is the set of induced k-rich $\delta $ -tubes, it can be shown that $|T| \sim \delta ^{-(d-1)}k^{d-1}$ . Further calculations show that

$$ \begin{align*} (S\delta^{-(d-1)} |A||T|)^{1/2} \sim S^{1/2} \delta^{-(d-1)} k^{d-1/{2}} \quad \text{and} \quad \delta^{-\alpha} S^{1-d}\mathcal{I}(A^S, T^S) \sim \delta^{-(d-1+\alpha)}k^d.\end{align*} $$

Also, since all tubes in T are k-rich, we have

$$ \begin{align*} \mathcal{I}(A,T) \sim \delta^{-(d-1)}k^d,\end{align*} $$

so the second term in Equation (2-1) is attained up to a $\delta ^{-\alpha }$ factor (for sufficiently small S).

Example 2.4. If $A \subset [0,1]^d$ consists of a $(d-1)$ -dimensional slice of the above configuration of $\delta $ -atoms, then we have $|A| \sim k^{d-1}$ . Again let T be the set of induced k-rich $\delta $ -tubes, so $|T| \sim \delta ^{-(d-1)}k^{d-3}$ . In this case,

$$ \begin{align*} (S\delta^{-(d-1)} |A||T|)^{1/2} \sim S^{1/2} \delta^{-(d-1)} k^{d-2} \quad \text{and} \quad \delta^{-\alpha}S^{1-d}\mathcal{I}(A^S, T^S) \sim S^{-1}\delta^{-(d-1+\alpha)}k^{d-2}.\end{align*} $$

Again, since all tubes in T are k-rich,

$$ \begin{align*} \mathcal{I}(A,T) \sim \delta^{-(d-1)}k^{d-2},\end{align*} $$

so the first term in Equation (2-1) is the attained bound up to an $S^{1/2}$ factor.

3 The main result

The proof of Theorem 1.4 combines induction with a cell partitioning argument. Often in proofs of incidence results it is useful to partition the space into smaller cells and estimate the contribution of incidences in each cell. An illustrative example is a very short, elementary proof of the Szemerédi–Trotter theorem for Cartesian products using a ‘lucky pairs’ argument. The prototype for this method can be found in [12].

The lucky pairs argument adapts readily to higher dimensions, and since our set of atoms A in $[0,1]^d$ is nearly a d-fold Cartesian product, we conjecture that the analogous bound should hold, namely that $|T_k(A)| \lesssim \delta ^{-\epsilon }|A|^2 k^{-(d+1)}$ .

We again mention that the higher-dimensional version of Theorem 1.4 does not follow from projecting into the plane and applying the $d=2$ result, since the well-distributed assumption that A is nearly grid-like is clearly violated after projection.

Our strategy is the following: we partition $[0,1]^d$ into cells of side length $D^{-1}$ for some parameter D to be chosen. Proposition 2.1 with some thickening parameter S allows us to relate the number of k-rich tubes to an incidence count, specifically the $L_2$ -norm of the weights of shortened tubes in all cells. This is bounded by applying the induction hypothesis in each cell.

For the proof to work, we need S to be much smaller than D, and D to be much smaller than $\delta ^{-\epsilon }$ . We also want S and D to be much bigger than constants. This is the motivation for the uniform choices of these parameters given in the proof.

The method is inspired by [11], but is different in several key ways. First, we work with incidences to give a new exposition of this kind of proof. Second, by using Proposition 2.1 which works for weighted atoms, we sidestep several dyadic pigeonholing steps which are needed in [11]. Finally, our problem admits an additional simplification. There is a simple expression for the number of $2$ -rich tubes induced by A which applies in any dimension $d\geq 2$ . This allows us to resolve both the ‘narrow’ and ‘broad’ case for small k which appear in [11], in a single simplified case.

Proof of Theorem 1.4.

We treat $\epsilon $ and d as constants, so in what follows, $\lesssim $ is written to mean $\lesssim _{\epsilon ,d}$ . We fix W and proceed by induction on $\delta $ . Namely, we have to prove the statement for all $\delta \in (0,W^{-1})$ . There are two base cases because when we apply the induction hypothesis, it will be for a smaller value of both W and $\delta ^{-1}$ .

The first base case will be when $\delta $ is very close to $W^{-1}$ , namely, when $\delta ^{-(1-c_1\epsilon )} \leq W$ for some small fixed $c_1$ (we choose $c_1<1/(d-1)$ which assists in the following calculation). Assuming $\delta ^{-(1-c_1\epsilon )} \leq W$ , Equation (1-4) gives

$$ \begin{align*} k \geq C_1(\epsilon,d) W^{d - ({d-1-\epsilon})/({1-c_1\epsilon})}> C_1(\epsilon,d) W.\end{align*} $$

Since the distribution of atoms permits $|T_k(A)|$ to be nonzero only if $k\lesssim W$ , we can choose $C_1({\epsilon },d)$ large enough so that $|T_k(A)| = 0$ , and Equation (1-5) holds trivially.

The other base case is when W is very small, say smaller than some constant $c_2$ . In this case, $|T_k(A)| \leq c_2^{2d}$ trivially, so Equation (1-5) holds for a suitable choice of $C_2(\epsilon ,d)$ .

We move on to the induction step. Assume the result holds for all $\delta '> K\delta $ and $W^{{\prime}{-1}}> KW^{-1}$ , where K is sufficiently small ( $K = 2$ will work). Assume Equation (1-4) holds.

First, we split up $[0,1]^d$ into $D^d$ sub-cubes or cells, where $D = \delta ^{-c_1^2 \epsilon ^2}$ . Let a tubelet be the intersection of a k-rich $\delta $ -tube with one of these cells. (A tubelet looks like a section of a $\delta $ -tube of length $D^{-1}$ .) To each tubelet t we associate a weight $w(t)$ which is the number of atoms from A intersecting t, and a multiplicity $m(t)$ which is the number of k-rich tubes containing the tubelet t. (A tubelet is ‘contained’ in a tube if all the atoms on the tubelet also intersect the tube. A tubelet may lie on up to $D^{d-1} k$ -rich tubes.) From here on, we often abbreviate $T_k = T_k(A)$ . With this notation, it is evident that

$$ \begin{align*} k|T_k| = \mathcal{I}(A,T_k) = \sum_{\text{tubelets }t} w(t)m(t). \end{align*} $$

It is also clear that

$$ \begin{align*}\sum_{\text{tubelets }t} m(t) = D|T_k|,\end{align*} $$

so by the pigeonhole principle, a positive proportion of the incidences come from tubelets t with $w(t) \gtrsim k/D$ (with an appropriate subsumed constant). We henceforth assume that the weights of all tubelets are at least $k/D$ .

Now we treat separately two cases: $k \lesssim D$ and $k \gtrsim D$ . The reason is that we will later apply the induction hypothesis to estimate the number of $k/D$ -rich tubelets, and the induction hypothesis only holds if $k/D$ is greater than some constant.

Case $1$ : $k\lesssim D$ . Since $D = \delta ^{-c_1^2\epsilon ^2}$ , it follows that $\delta ^{-\epsilon }k^{-3} \gtrsim 1$ . Now let us count the tubes that are at least $2$ -rich. For each pair of atoms $a,a'\in A$ , there are $\operatorname {\mathrm {dist}}(a,a')^{-(d-1)}$ tubes passing through both (where $\operatorname {\mathrm {dist}}(a,a')$ is the distance between the centres of atoms a and $a'$ ). It follows that

$$ \begin{align*}|T_k(A)| \leq |T_{\geq 2}(A)| = \sum_{\substack{{a,a' \in A} \\ {a \neq a'}}} \operatorname{\mathrm{dist}}(a,a')^{-(d-1)}.\end{align*} $$

By the grid-like configuration, we may assume that the atoms are exactly arranged in a d-dimensional integer grid (scaled down by a factor of W). At worst, this affects the above sum by a small multiplicative constant. We also lose no generality by considering only the case where $a'$ is the atom with centre at the origin. Thus, it follows that

$$ \begin{align*} \sum_{\substack{{a,a' \in A} \\ {a \neq a'}}} \operatorname{\mathrm{dist}}(a,a')^{-(d-1)} \sim |A|W^{d-1} \cdot \sum_{\substack{{\mathbf{n} \in (\mathbb{Z} \cap [0,W])^d} \\ {\mathbf{n} \neq 0}}} \| \mathbf{n}\| ^{-(d-1)}. \end{align*} $$

Given $x \in [0,W]$ , we have $\|\mathbf {n}\| \in [x,2x)$ for $\sim _d x^d$ values of $\mathbf {n}$ . Incorporating this into a dyadic sum, one obtains the desired

$$ \begin{align*} |T_k(A)| \lesssim_d |A|W^{d-1} \cdot \sum_{x \text{ dyadic}}^W x \lesssim \delta^{-\epsilon}\frac{|A|^2}{k^3}. \end{align*} $$

Case $2$ : $k \gtrsim D$ . We want to apply Proposition 2.1, but to do so globally is wasteful of the strong spacing assumptions on A, so the bound will be prohibitively weak.

If we consider any maximal set of distinct $D\delta $ -tubes in $[0,1]^d$ , then each $\delta $ -tube is contained in one of these $D\delta $ -tubes. Indeed, this partitions the set of all $\delta $ -tubes into the $D\delta $ -tubes which contain them. The rationale for this partitioning is that in each $D\delta $ -tube, the tubelets behave like weighted atoms. There are $(D\delta )^{-2(d-1)}$ such $D\delta $ -tubes.

Given one of these $D\delta $ -tubes $\tau $ , we ‘stretch’ it in all nonaxis directions by a factor of $D^{-1}\delta ^{-1}$ , so it becomes $[0,1]^d$ . Each tubelet in $\tau $ that runs parallel to $\tau $ becomes a $D^{-1}$ -atom, and each k-rich $\delta $ -tube in $\tau $ becomes a $D^{-1}$ -tube. Furthermore, each new atom has a weight, which is the same as the weight of the corresponding tubelet. Call this set of new weighted $D^{-1}$ -atoms $\mathbb {A}_\tau $ and the set of new $D^{-1}$ -tubes $\mathbb {T}_\tau $ . For the case $d=2$ , this procedure is indicated in Figure 1.

Figure 1 After ‘stretching’, the incidences between tubelets and $\delta $ -tubes inside a $D\delta $ -tube become incidences between weighted $D^{-1}$ -atoms and $D^{-1}$ -tubes.

For each $D\delta $ -tube $\tau $ , we count the incidences arising from tubelets that lie on, and are parallel to, $\tau $ . By the stretching procedure above (see Figure 1), this is equal to $\mathcal {I}(\mathbb {A}_\tau , \mathbb {T}_\tau )$ . It follows that

$$ \begin{align*}\mathcal{I}(A,T_k) = \sum_{\tau} \mathcal{I}(\mathbb{A}_\tau, \mathbb{T}_\tau).\end{align*} $$

Applying Proposition 2.1 in each $D\delta $ -tube $\tau $ using a thickening factor $S = \delta ^{-c_1^3\epsilon ^3}$ and $\delta ^{-\alpha } = S^\epsilon $ , and then applying Cauchy–Schwarz,

(3-1) $$ \begin{align} k|T_k| = \mathcal{I}(A,T_k) &= \sum_{\tau} \mathcal{I}(\mathbb{A}_\tau, \mathbb{T}_\tau) \nonumber \\ &\lesssim \sum_{\tau}\bigg(SD^{d-1}|\mathbb{T}_\tau|\sum_{a\in \mathbb{A}_\tau} w(a)^2\bigg)^{1/2} + S^{1-d+\epsilon} \sum_\tau \mathcal{I}(\mathbb{A}_\tau^S, \mathbb{T}_\tau^S) \nonumber \\ &\leq (SD^{d-1})^{1/2} \bigg(\sum_\tau |\mathbb{T}_\tau|\bigg)^{1/2} \bigg(\sum_\tau \sum_{a\in \mathbb{A}_\tau} w(a)^2\bigg)^{1/2} + S^{1-d+\epsilon} \mathcal{I}(A^S,T_k^S) \nonumber \\ &= (SD^{d-1})^{1/2} |T_k|^{1/2} \bigg(\sum_\tau \sum_{a\in \mathbb{A}_\tau} w(a)^2\bigg)^{1/2} + S^{1-d+\epsilon} \mathcal{I}(A^S,T_k^S). \end{align} $$

We now have two cases based on which term in Equation (3-1) dominates.

First suppose the second term dominates. Since there is at most one atom in each $W^{-1}$ -cell, all thickened $S\delta $ -atoms in $A^S$ have weight one, and hence $|A^S|= |A|$ . Also, the weights of tubes in $T^S$ are trivially bounded above by $S^{2(d-1)}$ , the maximum number of $\delta $ -tubes contained in an $S\delta $ -tube. If $\tilde {T}_k^S$ is the underlying set of unweighted tubes, then

(3-2) $$ \begin{align} \mathcal{I}(A^S,T_k^S) \lesssim S^{2(d-1)}\mathcal{I}(A^S,\tilde{T}_k^S). \end{align} $$

To have $k|T_k| \lesssim S^{1-d}\mathcal {I}(A^S,T_k^S)$ , a positive proportion of these incidences must be supported on $S\delta $ -tubes that are at least $S^{d-1}k$ -rich in atoms from $A^S$ . Furthermore, Equation (1-4) implies that

$$ \begin{align*}S^{d-1}k \geq S^{d-1} C_1(\epsilon,d)\delta^{d-1-\epsilon}|A| \geq C_1(\epsilon,d)(S\delta)^{d-1-\epsilon}|A^S| \cdot S^\epsilon,\end{align*} $$

so we can apply the induction hypothesis for any richness $k' \geq S^{d-1}k$ . Standard dyadic summing of the induction hypothesis implies that

(3-3) $$ \begin{align} \mathcal{I}(A^S,\tilde{T}_k^S) \lesssim C_2(\epsilon,d\,) (S\delta)^{-\epsilon} \frac{|A|^2}{(S^{d-1}k)^2}. \end{align} $$

Then combining Equations (3-1), (3-2) and (3-3) yields

$$ \begin{align*} k|T_k| \lesssim S^{1-d} C_2(\epsilon,d) \delta^{-\epsilon} \frac{|A|^2}{k^2}, \end{align*} $$

and rearranging closes the induction, as the $S^{1-d}$ term subsumes the multiplicative constants.

Now assume the first term in Equation (3-1) dominates. After rearranging, this implies that

(3-4) $$ \begin{align} |T_k| \lesssim \frac{SD^{d-1}(\sum_\tau \sum_{a\in \mathbb{A}_\tau} w(a)^2)}{k^2}. \end{align} $$

Notice that the bracketed term in the numerator is a sum over all tubelets. A suitable bound on this quantity will complete the proof.

Having already partitioned $[0,1]^d$ into $D^{d}$ cells, we now estimate the contribution from tubelets in each cell. For any of these cells $\mathcal {C}$ , let $A_{\mathcal {C}}$ be the set of atoms from A that lie in $\mathcal {C}$ and let $T_{\mathcal {C}}$ be the set of tubelets in $\mathcal {C}$ .

If we enlarge each cell $\mathcal {C}$ to $[0,1]^d$ , then the $\delta $ -atoms become $D\delta $ -atoms that satisfy the spacing conditions for applying the induction hypothesis. This technically assumes that $D < W$ ; the reverse case is simple and discussed at the end of the proof. Each tubelet t is now a $D\delta $ -tube, and the richness of this tube, denoted by $r(t)$ , is the weight of the corresponding tubelet. Recall that these weights all exceed $k/D$ . For any $m> k/D$ , using Equation (1-4),

$$ \begin{align*}m &> C_1(\epsilon,d) \delta^{d-1-\epsilon}|A| D^{-1} \\ & > C_1(\epsilon,d)(\delta D)^{d-1-\epsilon} (D^{-d}|A|) \\ & = C_1(\epsilon,d)(\delta D)^{d-1-\epsilon} |A_{\mathcal{C}}|, \end{align*} $$

so the induction hypothesis in Equation (1-5) can be used in any cell $\mathcal {C}$ to bound $|T_m(A_{\mathcal {C}})|$ . We get

$$ \begin{align*} \sum_{\tau} \sum_{a\in \mathbb{A}_\tau} w(a)^2 &= \sum_{\mathcal{C}} \sum_{t\in T_{\mathcal{C}}} r(t)^2 \\&=\sum_{\mathcal{C}} \sum_{\substack{{m \text{ dyadic}} \\ {m= k/D}}}^{k} m^2 |T_m(A_{\mathcal{C}})| \\&\leq \sum_{\mathcal{C}} \sum_{\substack{{m \text{ dyadic}} \\ {m= k/D}}}^{k} C_2(\epsilon,d)(D\delta)^{-\epsilon} (|A|D^{-d})^2 m^{-1} \\&\lesssim D^d \cdot C_2(\epsilon,d) (D\delta)^{-\epsilon} (|A|D^{-d})^2 \cdot(D/k). \end{align*} $$

Substituting this into Equation (3-4), and recalling that $S = \delta ^{-c_1^3\epsilon ^3}$ and $D = \delta ^{-c_1^2\epsilon ^2}$ ,

$$ \begin{align*} |T_k(A)| \leq C_2(\epsilon,d) \delta^{-\epsilon}|A|^2 k^{-3},\end{align*} $$

closing the induction and completing the proof.□

Remark 3.1. There is a small omission in the above proof: in Case 2, it is essential that each cell contains approximately the same number of atoms from A and that they are well distributed. This follows immediately if $D < W$ . However, if $D \geq W$ , then $\delta $ is so ridiculously small that the $\delta ^{-\epsilon }$ factor in Equation (1-5) is enormous, and trivial bounds give the desired result. Concretely, if $W \leq D = \delta ^{-c_1^2\epsilon ^2}$ , then since no pair of atoms can lie on more than W tubes,

$$ \begin{align*}|T_k(A)| \leq W|A|^2 \leq W^4 \cdot\frac{|A|^2}{k^3} \leq \delta^{-4c^2\epsilon^2} \cdot\frac{|A|^2}{k^3} \leq \delta^{-\epsilon} \cdot\frac{|A|^2}{k^3}.\end{align*} $$

4 An application

Beck’s theorem [1] is an important result in discrete geometry, and is a standard corollary of the Szemerédi–Trotter theorem. It states that given n points in the plane with at most $n-k$ on any line, the number of lines connecting at least two such points is $\gtrsim nk$ . Theorem 1.4 allows us to prove a version of Beck’s theorem for a set of well-spaced atoms in any dimension $d\geq 2$ . We use the same method that can be used to derive Beck’s theorem from the Szemerédi–Trotter theorem.

Theorem 4.1. Let A be a set of $\delta $ -atoms in $[0,1]^d$ satisfying the spacing conditions of Theorem 1.4, and such that $|A| \leq \delta ^{1-d}$ . Then for every $\epsilon> 0$ ,

$$ \begin{align*} |T_{\geq 2}(A)| \gtrsim_{\epsilon,d} \delta^{\epsilon}|A|^2.\end{align*} $$

Proof. Since $|A| \leq \delta ^{1-d}$ , Theorem 1.4 can be applied and

$$ \begin{align*}|T_k(A)| \leq C_2(\epsilon/2,d) \delta^{-\epsilon/2} \cdot \frac{|A|^2}{k^3}\end{align*} $$

holds for all k. The number of pairs of atoms that both lie on a tube that is at least $k_0$ -rich is given by

$$ \begin{align*}\sum_{\substack{{k \text{ dyadic}} \\ {k \geq k_0}}}k^2 |T_k(A)| \leq 2C_2(\epsilon/2,d) \delta^{-\epsilon/2}\frac{|A|^2}{k_0}.\end{align*} $$

Choosing $k_0 = 10 C_2(\epsilon /2,d)\delta ^{-\epsilon /2}$ , it follows that $\gtrsim _{\epsilon ,d}|A|^2$ pairs of atoms lie together only on tubes that are less than $k_0$ -rich. A $\delta $ -tube can have at most $k_0^2$ of these pairs lying on it so there are $\gtrsim _{\epsilon ,d} |A|^2/k_0^2 \sim \delta ^\epsilon |A|^2$ tubes that are at least $2$ -rich, completing the proof.