Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T15:42:17.788Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INTEGRAL REPRESENTATION FOR BESOV AND LIPSCHITZ SPACES

Part of: Spaces and algebras of analytic functions Holomorphic functions of several complex variables

Published online by Cambridge University Press:  17 October 2014

KEHE ZHU
KEHE ZHU*
Affiliation:
Department of Mathematics, SUNY at Albany, Albany, NY 12222, USA email kzhu@math.albany.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that functions in the analytic Besov space 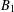$B_{1}$ on the unit disk 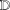$\mathbb{D}$ admit an integral representation

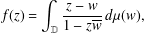$$\begin{eqnarray}f(z)=\int _{\mathbb{D}}\frac{z-w}{1-z\overline{w}}\,d{\it\mu}(w),\end{eqnarray}$$
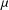where ${\it\mu}$ is a complex Borel measure with 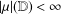$|{\it\mu}|(\mathbb{D})<\infty$. We generalize this result to all Besov spaces 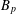$B_{p}$ with 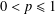$0<p\leq 1$ and all Lipschitz spaces 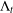${\rm\Lambda}_{t}$ with 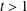$t>1$. We also obtain a version for Bergman and Fock spaces.

Keywords

Bergman spacesBesov spacesLipschitz spacesFock spacesCarleson measuresatomic decompositionBerezin transform

MSC classification

Primary: 30H20: Bergman spaces, Fock spaces
Secondary: 30H25: Besov spaces and $Q_p$-spaces 32A36: Bergman spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 1 , February 2015 , pp. 129 - 144
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Arazy, J. and Fisher, S., ‘Some aspects of the minimal, Möbius invariant space of analytic functions on the unit disk’, in: Interpolation Spaces and Allied Topics in Analysis (Lund, 1983), Springer Lecture Notes in Mathematics, 1070 (Springer, New York, 1984), 24–44.Google Scholar
Arazy, J., Fisher, S. and Peetre, J., ‘Möbius invariant function spaces’, J. reine angew. Math. 363 (1985), 110–145.Google Scholar
Beatrous, F. and Burbea, J., ‘Holomorphic Sobolev spaces on the ball’, Dissertationes Math. (Rozprawy Mat.) 276 (1989).Google Scholar
Coifman, R. and Rochberg, R., ‘Representation theorems for holomorphic and harmonic functions in L p’, Astérisque 77 (1980), 11–66.Google Scholar
Garnett, J., Bounded Analytic Functions (Academic Press, New York, 1981).Google Scholar
Janson, S., Peetre, J. and Rochberg, R., ‘Hankel forms and the Fock space’, Rev. Mat. Iberoam. 3 (1987), 61–138.CrossRefGoogle Scholar
Rudin, W., Function Theory in the Unit Ball of ℂn (Springer, New York, 1980).CrossRefGoogle Scholar
Wallstén, R., ‘The S p-criterion for Hankel forms on the Fock space, 0 < p < 1’, Math. Scand. 64 (1989), 123–132.CrossRefGoogle Scholar
Zhao, R. and Zhu, K., ‘Theory of Bergman spaces in the unit ball of ℂn’, Mém. Soc. Math. Fr. (N.S.) 115 (2008).Google Scholar
Zhu, K., Spaces of Holomorphic Functions in the Unit Ball (Springer, New York, 2005).Google Scholar
Zhu, K., Operator Theory in Function Spaces, 2nd edn (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar
Zhu, K., Analysis on Fock Spaces (Springer, New York, 2012).CrossRefGoogle Scholar