Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2008.
A variant of Cowling–Price's theorem for the Dunkl transform on R.
Journal of Mathematical Analysis and Applications,
Vol. 345,
Issue. 2,
p.
593.
Kawazoe, Takeshi
and
Mejjaoli, Hatem
2010.
Uncertainty principles for the Dunkl transform.
Hiroshima Mathematical Journal,
Vol. 40,
Issue. 2,
Chouchene, F.
Daher, R.
Kawazoe, T.
and
Mejjaoli, H.
2011.
Miyachi's theorem for the Dunkl transform.
Integral Transforms and Special Functions,
Vol. 22,
Issue. 3,
p.
167.
Hamem, Soumeya
Kamoun, Lotfi
and
Negzaoui, Selma
2013.
Cowling–Price type theorem related to Bessel–Struve transform.
Arab Journal of Mathematical Sciences,
Vol. 19,
Issue. 2,
p.
187.
Ghobber, Saifallah
2013.
Uncertainty principles involvingL1-norms for the Dunkl transform.
Integral Transforms and Special Functions,
Vol. 24,
Issue. 6,
p.
491.
Mejjaoli, Hatem
2013.
Dunkl-Schrödinger semigroups and applications.
Applicable Analysis,
Vol. 92,
Issue. 8,
p.
1597.
Mejjaoli, Hatem
2013.
Dunkl heat semigroup and applications.
Applicable Analysis,
Vol. 92,
Issue. 9,
p.
1980.
Soltani, Fethi
2014.
Pitt's inequalities for the Dunkl transform on ℝd.
Integral Transforms and Special Functions,
Vol. 25,
Issue. 9,
p.
686.
Mejjaoli, Hatem
2014.
Qualitative uncertainty principles for the Opdam–Cherednik transform.
Integral Transforms and Special Functions,
Vol. 25,
Issue. 7,
p.
528.
Parui, Sanjay
and
Pusti, Sanjoy
2015.
Revisiting Beurling's theorem for Fourier–Dunkl transform.
Integral Transforms and Special Functions,
Vol. 26,
Issue. 9,
p.
687.
Mejjaoli, Hatem
2015.
QUALITATIVE UNCERTAINTY PRINCIPLES FOR THE INVERSE OF THE HYPERGEOMETRIC FOURIER TRANSFORM.
Korean Journal of Mathematics,
Vol. 23,
Issue. 1,
p.
129.
Mejjaoli, H.
2015.
Qualitative uncertainty principles for the hypergeometric Fourier transform.
Acta Mathematica Hungarica,
Vol. 145,
Issue. 1,
p.
229.
Mejjaoli, Hatem
2015.
Cowling–Price’s and Hardy’s uncertainty Principles for the generalized Fourier transform associated to a Cherednik type operator on the real line.
Archiv der Mathematik,
Vol. 104,
Issue. 4,
p.
377.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2016.
Qualitative uncertainty principles for the generalized Fourier transform associated to a Dunkl type operator on the real line.
Analysis and Mathematical Physics,
Vol. 6,
Issue. 2,
p.
141.
Mejjaoli, Hatem
2016.
Uncertainty principles for the generalized Fourier transform associated to a Dunkl-type operator.
Applicable Analysis,
Vol. 95,
Issue. 9,
p.
1930.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2017.
A variant of Hardy's and Miyachi's theorems for the Bessel–Struve transform.
Integral Transforms and Special Functions,
Vol. 28,
Issue. 5,
p.
374.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2018.
A variant of Cowling–Price's and Miyachi's theorems for the Bessel–Struve transform on ℝd.
Journal of Taibah University for Science,
Vol. 12,
Issue. 4,
p.
415.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2018.
Boundedness and compactness of localization operators associated with the Dunkl–Wigner transform.
Integral Transforms and Special Functions,
Vol. 29,
Issue. 4,
p.
310.
Poria, Anirudha
2021.
Uncertainty principles for the Opdam–Cherednik transform on modulation spaces.
Integral Transforms and Special Functions,
Vol. 32,
Issue. 3,
p.
191.
Mondal, Shyam Swarup
and
Poria, Anirudha
2022.
Qualitative uncertainty principles for the windowed Opdam–Cherednik transform on weighted modulation spaces.
Mathematical Methods in the Applied Sciences,
Vol. 45,
Issue. 16,
p.
10424.

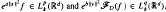 where
where 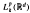 are the Lebesgue spaces associated with the Dunkl transform.
are the Lebesgue spaces associated with the Dunkl transform.