Published online by Cambridge University Press: 22 June 2021
In noncommutative algebraic geometry an Artin–Schelter regular (AS-regular) algebra is one of the main interests, and every three-dimensional quadratic AS-regular algebra is a geometric algebra, introduced by Mori, whose point scheme is either 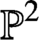 $\mathbb {P}^{2}$
or a cubic curve in
$\mathbb {P}^{2}$
or a cubic curve in 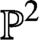 $\mathbb {P}^{2}$
by Artin et al. [‘Some algebras associated to automorphisms of elliptic curves’, in: The Grothendieck Festschrift, Vol. 1, Progress in Mathematics, 86 (Birkhäuser, Basel, 1990), 33–85]. In the preceding paper by the authors Itaba and Matsuno [‘Defining relations of 3-dimensional quadratic AS-regular algebras’, Math. J. Okayama Univ. 63 (2021), 61–86], we determined all possible defining relations for these geometric algebras. However, we did not check their AS-regularity. In this paper, by using twisted superpotentials and twists of superpotentials in the Mori–Smith sense, we check the AS-regularity of geometric algebras whose point schemes are not elliptic curves. For geometric algebras whose point schemes are elliptic curves, we give a simple condition for three-dimensional quadratic AS-regular algebras. As an application, we show that every three-dimensional quadratic AS-regular algebra is graded Morita equivalent to a Calabi–Yau AS-regular algebra.
$\mathbb {P}^{2}$
by Artin et al. [‘Some algebras associated to automorphisms of elliptic curves’, in: The Grothendieck Festschrift, Vol. 1, Progress in Mathematics, 86 (Birkhäuser, Basel, 1990), 33–85]. In the preceding paper by the authors Itaba and Matsuno [‘Defining relations of 3-dimensional quadratic AS-regular algebras’, Math. J. Okayama Univ. 63 (2021), 61–86], we determined all possible defining relations for these geometric algebras. However, we did not check their AS-regularity. In this paper, by using twisted superpotentials and twists of superpotentials in the Mori–Smith sense, we check the AS-regularity of geometric algebras whose point schemes are not elliptic curves. For geometric algebras whose point schemes are elliptic curves, we give a simple condition for three-dimensional quadratic AS-regular algebras. As an application, we show that every three-dimensional quadratic AS-regular algebra is graded Morita equivalent to a Calabi–Yau AS-regular algebra.
Communicated by Daniel Chan
The first author was supported by Grants-in-Aid for Young Scientific Research 18K13397 Japan Society for the Promotion of Science.