Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T05:02:13.988Z Has data issue: false hasContentIssue false
  • English
  • Français

BALANCE FOR TATE COHOMOLOGY WITH RESPECT TO SEMIDUALIZING MODULES

Part of: Homological algebra Commutative algebra: Homological methods

Published online by Cambridge University Press:  18 July 2013

LI LIANG  and
GANG YANG
LI LIANG*
Affiliation:
School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, PR China email yanggang@mail.lzjtu.cn
GANG YANG
Affiliation:
School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, PR China email yanggang@mail.lzjtu.cn
*
✉lliangnju@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we further study Tate cohomology of modules over a commutative ring with respect to semidualizing modules using the ideals of Sather-Wagstaff et al. [‘Tate cohomology with respect to semidualizing modules’, J. Algebra 324 (2010), 2336–2368]. In particular, we prove a balance result for the Tate cohomology 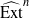${\widehat{\mathrm{Ext} }}^{n} $ for any $n\in \mathbb{Z} $. This result complements the work of Sather-Wagstaff et al., who proved that the result holds for any 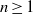$n\geq 1$. We also discuss some vanishing properties of Tate cohomology.

Keywords

Tate cohomologyrelative cohomologybalancesemidualizing modules

MSC classification

Secondary: 13D07: Homological functors on modules (Tor, Ext, etc.) 18G15: Ext and Tor, generalizations, Künneth formula 18G25: Relative homological algebra, projective classes 13D02: Syzygies, resolutions, complexes 13D05: Homological dimension 18G10: Resolutions; derived functors 18G20: Homological dimension
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 2 , October 2013 , pp. 223 - 240
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Avramov, L. L. and Martsinkovsky, A., ‘Absolute, relative, and Tate cohomology of modules of finite Gorenstein dimension’, Proc. Lond. Math. Soc. 85 (2002), 393–440.CrossRefGoogle Scholar
Christensen, L. W., Frankild, A. and Holm, H., ‘On Gorenstein projective, injective and flat dimensions—a functorial description with applications’, J. Algebra 302 (2006), 231–279.CrossRefGoogle Scholar
Christensen, L. W. and Jorgensen, D. A., ‘Tate (co)homology via pinched complexes’, Trans. Amer. Math. Soc.; doi:10.1090/S0002-9947-2013-05746-7.CrossRefGoogle Scholar
Enochs, E. E., Estrada, S. and Iacob, A., ‘Balance with unbounded complexes’, Bull. Lond. Math. Soc. 44 (2012), 439–442.CrossRefGoogle Scholar
Holm, H., ‘Gorenstein derived functors’, Proc. Amer. Math. Soc. 132 (2004), 1913–1923.CrossRefGoogle Scholar
Iacob, A., ‘Generalized Tate cohomology’, Tsukuba J. Math. 29 (2005), 389–404.CrossRefGoogle Scholar
Sather-Wagstaff, S., Sharif, T. and White, D., ‘Stability of Gorenstein categories’, J. Lond. Math. Soc. 77 (2008), 481–502.CrossRefGoogle Scholar
Sather-Wagstaff, S., Sharif, T. and White, D., ‘Gorenstein cohomology in abelian categories’, J. Math. Kyoto Univ. 48 (2008), 571–596.Google Scholar
Sather-Wagstaff, S., Sharif, T. and White, D., ‘Tate cohomology with respect to semidualizing modules’, J. Algebra 324 (2010), 2336–2368.CrossRefGoogle Scholar