Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T14:16:22.406Z Has data issue: false hasContentIssue false
  • English
  • Français

BELLWETHERS FOR BOUNDEDNESS OF COMPOSITION OPERATORS ON WEIGHTED BANACH SPACES OF ANALYTIC FUNCTIONS

Part of: Special classes of linear operators

Published online by Cambridge University Press:  01 June 2009

PAUL S. BOURDON
PAUL S. BOURDON*
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA 24450, USA (email: pbourdon@wlu.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 𝔻 be the open unit disc, let v:𝔻→(0,∞) be a typical weight, and let Hv∞ be the corresponding weighted Banach space consisting of analytic functions f on 𝔻 such that 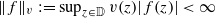. We call Hv∞ a typical-growth space. For ϕ a holomorphic self-map of 𝔻, let Cφ denote the composition operator induced by ϕ. We say that Cφ is a bellwether for boundedness of composition operators on typical-growth spaces if for each typical weight v, Cφ acts boundedly on Hv∞ only if all composition operators act boundedly on Hv∞. We show that a sufficient condition for Cφ to be a bellwether for boundedness is that ϕ have an angular derivative of modulus less than 1 at a point on ∂𝔻. We raise the question of whether this angular-derivative condition is also necessary for Cφ to be a bellwether for boundedness.

Keywords

composition operatorweighted Bergman space of infinite orderboundednessangular derivativeLusky condition

MSC classification

Secondary: 47B33: Composition operators
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 86 , Issue 3 , June 2009 , pp. 305 - 314
Copyright
Copyright © Australian Mathematical Society 2009

References

[1]Aron, R. and Lindström, M., ‘Spectra of weighted composition operators on weighted Banach spaces of analytic functions’, Israel J. Math. 141 (2004), 263–276.CrossRefGoogle Scholar
[2]Bierstedt, K. D., Bonet, J. and Taskinen, J., ‘Associated weights and spaces of holomorphic functions’, Studia Math. 127 (1998), 137–168.CrossRefGoogle Scholar
[3]Bonet, J., Domański, P. and Lindström, M., ‘Essential norm and weak compactness of composition operators on weighted Banach spaces of analytic functions’, Canad. Math. Bull. 42 (1999), 139–148.CrossRefGoogle Scholar
[4]Bonet, J., Domański, P., Lindström, M. and Taskinen, J., ‘Composition operators between weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Series A) 64 (1998), 101–118.Google Scholar
[5]Contreras, M. D. and Hernandez-Diaz, A. G., ‘Weighted composition operators in weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Series A) 69 (2000), 41–60.Google Scholar
[6]Cowen, C. and MacCluer, B., Composition Operators on Spaces of Analytic Functions (CRC Press, Boca Raton, FL, 1995).Google Scholar
[7]Lusky, W., ‘On weighted spaces of harmonic and holomorphic functions’, J. London Math. Soc. 51 (1995), 309–320.CrossRefGoogle Scholar
[8]Montes-Rodríguez, A., ‘Weighted composition operators on weighted Banach spaces of analytic functions’, J. London Math. Soc. 61 (2000), 872–884.CrossRefGoogle Scholar
[9]Shapiro, J. H., Composition Operators and Classical Function Theory (Springer-Verlag, Berlin, 1993).CrossRefGoogle Scholar