Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T06:21:26.980Z Has data issue: false hasContentIssue false
  • English
  • Français

b-GENERALIZED DERIVATIONS OF SEMIPRIME RINGS HAVING NILPOTENT VALUES

Part of: Rings with polynomial identity Rings and algebras with additional structure Radicals and radical properties of rings

Published online by Cambridge University Press:  31 March 2014

M. TAMER KOŞAN  and
TSIU-KWEN LEE
M. TAMER KOŞAN
Affiliation:
Department of Mathematics, Gebze Institute of Technology, 41400 Gebze/Kocaeli, Turkey email mtkosan@gyte.edu.tr
TSIU-KWEN LEE*
Affiliation:
Department of Mathematics, National Taiwan University, Taipei, Taiwan email tklee@math.ntu.edu.tw
*
✉tklee@math.ntu.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

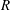Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a semiprime ring with extended centroid 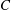$C$ and with maximal right ring of quotients 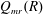$Q_{mr}(R)$. Let 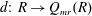$d{:}\ R\to Q_{mr}(R)$ be an additive map and 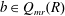$b\in Q_{mr}(R)$. An additive map 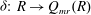$\delta {:}\ R\to Q_{mr}(R)$ is called a (left) 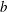$b$-generalized derivation with associated map 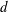$d$ if 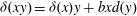$\delta (xy)=\delta (x)y+bxd(y)$ for all 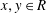$x, y\in R$. This gives a unified viewpoint of derivations, generalized derivations and generalized $\sigma $-derivations with an X-inner automorphism $\sigma $. We give a complete characterization of $b$-generalized derivations of $R$ having nilpotent values of bounded index. This extends several known results in the literature.

Keywords

prime ringsemiprime ringGPI(generalized) σ-derivationb-generalized derivationorthogonal completion

MSC classification

Secondary: 16N60: Prime and semiprime rings 16R50: Other kinds of identities (generalized polynomial, rational, involution) 16W25: Derivations, actions of Lie algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 3 , June 2014 , pp. 326 - 337
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Beidar, K. I., Martindale III, W. S. and Mikhalev, A. V., Rings with Generalized Identities, Monographs and Textbooks in Pure and Applied Mathematics, 196 (Marcel Dekker, Inc, New York, 1996).Google Scholar
Brešar, M., ‘On the distance of the composition of two derivations to the generalized derivations’, Glasg. Math. J. 33(1) (1991), 89–93.Google Scholar
Chang, J. C., ‘Generalized skew derivations with nilpotent values on Lie ideals’, Monatsh. Math. 161(2) (2010), 155–160.Google Scholar
Chang, J. C., ‘Generalized skew derivations with power central values on Lie ideals’, Comm. Algebra 39(6) (2011), 2241–2248.Google Scholar
Chang, J. C. and Lin, J. S., ‘(α, β)-derivations with nilpotent values’, Chinese J. Math. 22(4) (1994), 349–355.Google Scholar
Chuang, C.-L., ‘GPIs having coefficients in Utumi quotient rings’, Proc. Amer. Math. Soc. 103 (1988), 723–728.CrossRefGoogle Scholar
Chuang, C.-L. and Lee, T.-K., ‘Derivations modulo elementary operators’, J. Algebra 338 (2011), 56–70.Google Scholar
Erickson, T. S., Martindale III, W. S. and Osborn, J. M., ‘Prime nonassociative algebras’, Pacific J. Math. 60(1) (1975), 49–63.Google Scholar
Faith, C. and Utumi, Y., ‘On a new proof of Litoff’s theorem’, Acta Math. Acad. Sci. Hung. 14 (1967), 369–371.Google Scholar
Giambruno, A. and Herstein, I. N., ‘Derivations with nilpotent values’, Rend. Circ. Mat. Palermo (2) 30(2) (1981), 199–206.CrossRefGoogle Scholar
Herstein, I. N., Topics in Ring Theory (The University of Chicago Press, Chicago, Ill.-London, 1969).Google Scholar
Herstein, I. N., ‘Center-like elements in prime rings’, J. Algebra 60 (1979), 567–574.Google Scholar
Herstein, I. N., ‘Derivations of prime rings having power central values’, in: Algebraists’ Homage: Papers in Ring Theory and Related Topics (New Haven, Conn., 1981), Contemporary Mathematics, 13 (American Mathematical Society, Providence, RI, 1982), 163–171.Google Scholar
Hvala, B., ‘Generalized derivations in rings’, Comm. Algebra 26(4) (1998), 1147–1166.Google Scholar
Kharchenko, V. K., ‘Differential identities of semiprime rings’, Algebra Logika 18 (1979), 86–119; Algebra Logic 18 (1979), 58–80 (English translation).CrossRefGoogle Scholar
Lanski, C., ‘Derivations with nilpotent values on left ideals’, Comm. Algebra 22(4) (1994), 1305–1320.Google Scholar
Lee, T.-K., ‘Semiprime rings with differential identities’, Bull. Inst. Math. Acad. Sin. 20 (1992), 27–38.Google Scholar
Lee, T.-K., ‘Generalized derivations of left faithful rings’, Comm. Algebra 27(8) (1999), 4057–4073.CrossRefGoogle Scholar
Lee, T.-K., ‘Generalized skew derivations characterized by acting on zero products’, Pacific J. Math. 216(2) (2004), 293–301.Google Scholar
Lee, T.-K. and Liu, K.-S., ‘The Skolem-Noether theorem for semiprime rings satisfying a strict identity’, Comm. Algebra 35(6) (2007), 1949–1955.Google Scholar
Lee, T.-K. and Liu, K.-S., ‘Generalized skew derivations with algebraic values of bounded degree’, Houston J. Math. 39(3) (2013), 733–740.Google Scholar
Lee, T.-K. and Zhou, Y., ‘An identity with generalized derivations’, J. Algebra Appl. 8(3) (2009), 307–317.Google Scholar
Martindale III, W. S., ‘Prime rings satisfying a generalized polynomial identity’, J. Algebra 12 (1969), 576–584.Google Scholar
Xu, X., Ma, J. and Niu, F., ‘Annihilators of power central values of generalized derivations’, Adv. Math. (China) 41(1) (2012), 113–119.Google Scholar