Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T04:05:49.107Z Has data issue: false hasContentIssue false
  • English
  • Français

BOUNDARY ANGULAR DERIVATIVES OF GENERALIZED SCHUR FUNCTIONS

Part of: General theory of linear operators

Published online by Cambridge University Press:  08 March 2013

VLADIMIR BOLOTNIKOV ,
TENGYAO WANG  and
JOSHUA M. WEISS
VLADIMIR BOLOTNIKOV*
Affiliation:
Department of Mathematics, The College of William and Mary, Williamsburg, VA, USA
TENGYAO WANG
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ, USA email tengyaow@princeton.edu
JOSHUA M. WEISS
Affiliation:
Department of Mathematics, Haverford College, Haverford, PA, USA email jweiss@haverford.edu
*
✉vladi@math.wm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Characterization of generalized Schur functions in terms of their Taylor coefficients was established by Krein and Langer [‘Über einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume 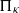${\Pi }_{\kappa } $ zusammenhängen. I. Einige Funktionenklassen und ihre Darstellungen’, Math. Nachr. 77 (1977), 187–236]. We establish a boundary analogue of this characterization.

Keywords

boundary interpolationangular derivativesgeneralized Schur functions

MSC classification

Secondary: 47A57: Operator methods in interpolation, moment and extension problems 47A20: Dilations, extensions, compressions 47A48: Operator colligations (= nodes), vessels, linear systems, characteristic functions, realizations, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 93 , Issue 3 , December 2012 , pp. 203 - 224
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ball, J. A., ‘Interpolation problems of Pick–Nevanlinna and Loewner type for meromorphic matrix functions’, Integral Equations Operator Theory 6 (1983), 804–840.CrossRefGoogle Scholar
Ball, J. A., Gohberg, I. and Rodman, L., Interpolation of Rational Matrix Functions (Birkhäuser Verlag, Basel, 1990).CrossRefGoogle Scholar
Ball, J. A. and Helton, J. W., ‘Interpolation problems of Pick–Nevanlinna and Loewner types for meromorphic matrix–functions: parametrization of the set of all solutions’, Integral Equations Operator Theory 9 (1986), 155–203.CrossRefGoogle Scholar
Bolotnikov, V., ‘A uniqueness result on boundary interpolation’, Proc. Amer. Math. Soc. 136 (5) (2008), 1705–1715.CrossRefGoogle Scholar
Bolotnikov, V., ‘On higher order boundary derivatives of an analytic self-map of the unit disk’, J. Approx. Theory 163 (4) (2011), 568–589.CrossRefGoogle Scholar
Bolotnikov, V. and Dym, H., ‘On boundary interpolation for matrix Schur functions’, Mem. Amer. Math. Soc. 181 (2006), 856.Google Scholar
Bolotnikov, V. and Kheifets, A., ‘The higher order Carathéodory–Julia theorem and related boundary interpolation problems’, Oper. Theory Adv. Appl. OT 179 (2007), 63–102.Google Scholar
Bolotnikov, V. and Kheifets, A., ‘Carathéodory–Julia type conditions and symmetries of boundary asymptotics for analytic functions on the unit disk’, Math. Nachr. 282 (11) (2009), 1513–1536.CrossRefGoogle Scholar
Bolotnikov, V., Kheifets, A. and Rodman, L., ‘Jet functions having indefinite Carathéodory-Pick matrices’, Linear Algebra Appl. 385 (2004), 215–286.CrossRefGoogle Scholar
Bolotnikov, V. and Zobin, N., ‘Boundary asymptotic expansions of analytic self-maps of the unit disk’, Rev. Mat. Iberoam., to appear.Google Scholar
Kovalishina, I. V., ‘A multiple boundary interpolation problem for contractive matrix–valued functions in the unit circle’, Teor. Funktsii, Funktsional. Anal. i Ikh Prilozhen. 51 (1989), 38–55; Engl. transl. J. Soviet Math. 52(6) (1990), 3467–3481.Google Scholar
Kreĭn, M. G. and Langer, H., ‘Über die verallgemeinerten Resolventen und die charakteristische Funktion eines isometrischen Operators im Raume ${\Pi }_{\kappa } $’, Colloq. Math. Soc. János Bolyai 5 (1972), 353–399.Google Scholar
Kreĭn, M. G. and Langer, H., ‘Über einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume ${\Pi }_{\kappa } $ zusammenhängen. I. Einige Funktionenklassen und ihre Darstellungen’, Math. Nachr. 77 (1977), 187–236.CrossRefGoogle Scholar
Schur, I., ‘Über Potenzreihen, die im Innern des Einheitskreises beschränkt sind’, J. reine angew. Math. 147 (1917), 205–232.CrossRefGoogle Scholar
Takagi, T., ‘On an algebraic problem related to an analytic theorem of Carathéodory and Fejér and on an allied theorem of Landau’, Jpn J. Math. 1 (1924), 83–93.CrossRefGoogle Scholar