Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T06:54:19.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of vector-valued martingale transforms on extreme points and applciations

Part of: Probability theory on algebraic and topological structures Stochastic processes Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  09 April 2009

Teresa Martínez  and
José L. Torrea
José L. Torrea
Affiliation:
Departmento de Matemáticas, Universidad Autónoma de MadridCiudad Universitaria de Canto Blanco 28049 Madrid, Spain, e-mail: teresa.martinez@uam.es, joseluis.torrea@uam.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Β1, Β2 be a pair of Banach spaces and T be a vector valued martingale transform (with respect to general filtration) which maps Β1-valued martingales into Β2-valued martingales. Then, the following statements are equivalent: T is bounded from 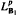into 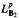for some p (or equivalently for every p) in the range 1 < p < ∞; T is bounded from 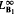into BMOB2; T is bounded from BMOB1 into BMOB2; T is bounded from 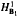into 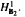. Applications to UMD and martingale cotype properties are given. We also prove that the Hardy space 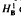defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.

Keywords

Martingale transformsHardy spacesBMO

MSC classification

Secondary: 60G42: Martingales with discrete parameter 60B11: Probability theory on linear topological spaces 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 76 , Issue 2 , April 2004 , pp. 207 - 222
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Bennet, C., De Vore, R. A. and Sharpley, R., ‘Weak-L ∞ and BMO’, Ann. of Math. (2) 113 (1981), 601–611.CrossRefGoogle Scholar
[2]Blasco, O., ‘Hardy spaces of vector-valued functions: duality’, Trans. Amer. Math. Soc. 308 (1988), 495–507.CrossRefGoogle Scholar
[3]Blasco, O. and García-Cuerva, J., ‘Hardy spaces of Banach-space-valued distributions’, Math. Nachr. 132 (1987), 57–65.CrossRefGoogle Scholar
[4]Bourgain, J., ‘Extension of a result of Benedeck, Calderon and Panzone’, Ark. Mat. 22 (1984), 91–95.CrossRefGoogle Scholar
[5]Bourgain, J., ‘Vector valued singular integrals and the H1 –BMO duality’, in: Israel seminar on geometrical aspects of functional analysis (1983/84) XVI (Tel Aviv Univ., Tel Aviv, 1984) pp. 1–23.Google Scholar
[6]Burkholder, D. L., ‘Martingale transforms’, Ann. Math. Statist. 37 (1966), 1494–1504.CrossRefGoogle Scholar
[7]Burkholder, D. L., ‘A geometrical characterization of Banach spaces in which martingale difference sequences are unconditional’, Ann. Probab. (9) 6 (1981), 997–1011.Google Scholar
[8]Chatterji, S. D., ‘Martingale convergence and the Radon-Nikodým theorem in Banach spaces’, Math. Scand. 22 (1968), 21–41.CrossRefGoogle Scholar
[9]Diestel, J. and Uhl, J. J., Vector measures, Math. Surveys 15 (Amer. Math. Soc., Providence 1977).CrossRefGoogle Scholar
[10]Doob, J. L., Stochastic processes (Wiley, New York, 1953).Google Scholar
[11]Garsia, A. M., Martingale inequalities. Seminar notes on recent progress, Math. Lecture Notes Ser. (Benjamin, New York, 1973).Google Scholar
[12]Herz, C., ‘Bounded mean oscillation and regulated martingales’, Trans. Amer. Math. Soc. 193 (1974), 199–215.CrossRefGoogle Scholar
[13]Martinez, T., ‘Uniform convexity in terms of martingale H 1 and BMO spaces’, Houston J. Math. 27 (2001), 461–478.Google Scholar
[14]Martinez, T. and Torrea, J. L., ‘Operator-valued martingale transforms’, Tohoku Math. J. 52 (2000), 449–474.CrossRefGoogle Scholar
[15]Pisier, G., ‘Martingales with values in uniformly convex spaces’, Israel J. Math. 20 (1975), 326–350.CrossRefGoogle Scholar
[16]Pisier, G., Probabilistic methods in the geometry of Banach spaces, Lecture Notes in Math. 1206 (Springer, Berlin, 1986).CrossRefGoogle Scholar
[17]Weisz, F., Martingale Hardy spaces and its applications in Fourier Analysis, Lecture Notes in Math. 1568 (Springer, Berlin, 1994).Google Scholar
[18]Weisz, F., ‘Martingale operators and Hardy spaces generated by them’, Studia Math. 114 (1995), 39–70.CrossRefGoogle Scholar
[19]Xu, Q., ‘Littlewood-Paley theory for functions with values in uniformly convex spaces’, J. Reine Angew. Math. 504 (1998), 195–226.CrossRefGoogle Scholar