Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T02:54:33.360Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for nilpotent-by-finite groups in certain varieties

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

G. Endimioni
G. Endimioni
Affiliation:
C.M.I., Université de Provence, UMR-CNRS 6632, 39, rue F. Joliot-Curie, 13453 Marseille Cedex 13, France e-mail: endimion@gyptis.univ-mrs.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

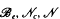Let and 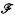denote respectively the variety of groups of exponent dividing e, the variety of nilpotent groups of class at most c, the class of nilpotent groups and the class of finite groups. It follows from a result due to Kargapolov and Čurkin and independently to Groves that in a variety not containing all metabelian groups, each polycyclic group G belongs to 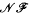. We show that G is in fact in 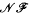, where c is an integer depending only on the variety. On the other hand, it is not always possible to find an integer e (depending only on the variety) such that G belongs to 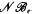but we characterize the varieties in which that is possible. In this case, there exists a function f such that, if G is d-generated, then G ∈ 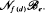So, when e = 1, we obtain an extension of Zel'manov's result about the restricted Burnside problem (as one might expect, this result is used in our proof). Finally, we show that the class of locally nilpotent groups of a variety 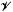forms a variety if and only if 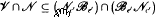for some integers c′, e′.

MSC classification

Secondary: 20E10: Quasivarieties and varieties of groups 20F18: Nilpotent groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 73 , Issue 3 , December 2002 , pp. 393 - 404
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Black, S., ‘Which words spell ‘almost nilpotent’?’, J. Algebra 221 (1999), 475–496.CrossRefGoogle Scholar
[2]Brandl, R., ‘On groups with small Engel depth’, Bull. Austral. Math. Soc. 28 (1983), 101–110.CrossRefGoogle Scholar
[3]Burns, R., Macedońska, O. and Medvedev, Y., ‘Groups satisfying semigroup laws and nilpotent-by-Burnside varieties’, J. Algebra 195 (1997), 510–525.CrossRefGoogle Scholar
[4]Burns, R. and Medvedev, Y., ‘A note on Engel groups and local nilpotence’, J. Austral. Math. Soc. (Series A) 64 (1998), 92–100.CrossRefGoogle Scholar
[5]Chapuis, O., ‘Variétés de groupes et m-identités’, C. R. Acad. Sci. Paris Sér. I Math. 316 (1993), 15–17.Google Scholar
[6]Endimioni, G., ‘On the locally finite p-groups in certain varieties of groups’, Quart. J. Math. Oxford 48 (1997), 169–178.CrossRefGoogle Scholar
[7]Endimioni, G., ‘On conditions for a group to satisfy given laws’, J. Group Theory 2 (1999), 191–198.CrossRefGoogle Scholar
[8]Groves, J. R. J., ‘On varieties of soluble groups. II’, Bull. Austral. Math. Soc. 7 (1972), 437–441.CrossRefGoogle Scholar
[9]Hall, P., ‘Finite-by-nilpotent groups’, Proc. Cambridge Philos. Soc. 52 (1956), 611–616.CrossRefGoogle Scholar
[10]Kargapolov, M. I. and Čturkin, V. A., ‘Varieties of solvable groups’, Algebra i Logika 10 (1971), 651–657.Google Scholar
[11]Lewin, J. and Lewin, T., ‘Semigroup laws in varieties of solvable groups’, Proc. Cambridge Philos. Soc. 65 (1969), 1–9.CrossRefGoogle Scholar
[12]Point, F., ‘Conditions of quasi-nilpotency in certain varieties of groups’, Comm. Algebra 22 (1994), 355–370.CrossRefGoogle Scholar
[13]Point, F., ‘Milnor identities’, Comm. Algebra 24 (1996), 3725–3744.CrossRefGoogle Scholar
[14]Robinson, D. J. S., A course in the theory of groups (Springer, New York, 1982).CrossRefGoogle Scholar
[15]Shalev, A., ‘Combinatorial conditions in residually finite groups, II’, J. Algebra 157 (1993), 51–62.CrossRefGoogle Scholar
[16]Vaughan-Lee, M., The restricted Burnside problem (Clarendon Press, Oxford, 1990).Google Scholar
[17]Wilson, J. S., ‘Two-generator conditions for residually finite groups’, Bull. London Math. Soc. (1991), 239–248.CrossRefGoogle Scholar
[18]Zel'manov, E. I., ‘On some problems of group theory and Lie algebras’, Math. USSR Sbornik (1990), 159–168.Google Scholar
[19]Zel'manov, E. I., ‘Solution of the restricted Burnside problem for groups of odd exponent’, Izv. Akad. Nauk. SSSR Ser. Mat. 54 (1990), 42–59.Google Scholar
[20]Zel'manov, E. I., ‘Solution of the restricted Burnside problem for 2-groups’, Mat. Sb. 182 (1991), 568–592.Google Scholar