Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T17:07:36.707Z Has data issue: false hasContentIssue false
  • English
  • Français

CARTAN–EILENBERG FP-INJECTIVE COMPLEXES

Part of: Homological algebra

Published online by Cambridge University Press:  23 December 2016

BO LU  and
ZHONGKUI LIU
BO LU*
Affiliation:
College of Mathematics and Computer Science, Northwest University for Nationalities, Lanzhou 730030, Gansu, PR China email lubo55@126.com
ZHONGKUI LIU
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, Gansu, PR China email liuzk@nwnu.edu.cn
*
✉lubo55@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we extend the notion of FP-injective modules to that of Cartan–Eilenberg complexes. We show that a complex 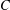$C$ is Cartan–Eilenberg FP-injective if and only if 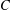$C$ and 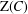$\text{Z}(C)$ are complexes consisting of FP-injective modules over right coherent rings. As an application, coherent rings are characterized in various ways, using Cartan–Eilenberg FP-injective and Cartan–Eilenberg flat complexes.

Keywords

Cartan–Eilenberg FP-injective complexCartan–Eilenberg flat complexcoherent ring

MSC classification

Primary: 18G35: Chain complexes
Secondary: 18G15: Ext and Tor, generalizations, Künneth formula
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 387 - 401
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by the National Natural Science Foundation of China (No. 11501451), the Fundamental Research Funds for the Central Universities (No. 31920150038) and XBMUYJRC (No. 201406).

References

Adams, D. D., ‘Absolutely pure modules’, PhD Thesis, University of Kentucky, 1978.Google Scholar
Beligiannis, A., ‘Relative homological algebra and purity in triangulated categories’, J. Algebra 227 (2000), 268–361.Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Chase, S., ‘Direct products of modules’, Trans. Amer. Math. Soc. 97 (1960), 457–473.Google Scholar
Chen, J. L. and Ding, N. Q., ‘The weak global dimension of commutative coherent rings’, Comm. Algebra 21(10) (1993), 3521–3528.Google Scholar
Chen, J. L. and Ding, N. Q., ‘On n-coherent rings’, Comm. Algebra 24(10) (1996), 3211–3216.Google Scholar
Chen, J. L. and Ding, N. Q., ‘Characterizations of coherent rings’, Comm. Algebra 27(5) (1999), 2491–2501.Google Scholar
Christensen, L. W., Foxby, H. B. and Holm, H., ‘Derived category methods in commutative algebra’, Preprint, 2011.Google Scholar
Enochs, E. E., ‘Cartan–Eilenberg complexes and resolutions’, J. Algebra 342 (2011), 16–39.Google Scholar
García Rozas, J. R., Covers and Envelopes in the Category of Complexes (CRC Press, Boca Raton, FL, 1999).Google Scholar
Glaz, S., Commutative Coherent Rings, Lecture Notes in Mathematics, 1371 (Springer, Berlin, 1989).Google Scholar
Jain, C., ‘Flat and FP-injectivity’, Proc. Amer. Math. Soc. 41 (1973), 437–442.Google Scholar
Lu, B. and Liu, Z. K., ‘Cartan–Eilenberg complexes with respect to cotorsion pairs’, Arch. Math. (Basel) 102 (2014), 35–48.Google Scholar
Lu, B., Ren, W. and Liu, Z. K., ‘A note on Cartan–Eilenberg Gorenstein categories’, Kodai Math. J. 38 (2015), 209–227.Google Scholar
Maddox, B. H., ‘Absolutely pure modules’, Proc. Amer. Math. Soc. 18 (1967), 155–158.Google Scholar
Mao, L. X. and Ding, N. Q., ‘Weak global dimension of coherent rings’, Comm. Algebra 35(12) (2007), 4319–4327.Google Scholar
Matlis, E., ‘Commutative coherent rings’, Canad. J. Math. 34(6) (1982), 1240–1244.Google Scholar
Megibben, C., ‘Absolutely pure modules’, Proc. Amer. Math. Soc. 26 (1970), 561–566.Google Scholar
Pinzon, K. R., ‘Absolutely pure modules’, PhD Thesis, University of Kentucky, 2005.Google Scholar
Pinzon, K. R., ‘Absolutely pure covers’, Comm. Algebra 36 (2008), 2186–2194.Google Scholar
Stenström, B., ‘Coherent rings and FP-injective modules’, J. Lond. Math. Soc. 2 (1970), 323–329.Google Scholar
Stenström, S., Rings of Quotients (Springer, Berlin, 1975).Google Scholar
Verdier, J. L., ‘Des catégories dérivées des catégories abéliennes’, Astérisque 239 (1997), 1–253.Google Scholar
Wang, Z. P. and Liu, Z. K., ‘FP-injective complexes and FP-injective dimension of complexes’, J. Aust. Math. Soc. 91 (2011), 163–187.CrossRefGoogle Scholar
Wisbauer, R., Foundations of Module and Ring Theory, Algebra, Logic and Applications Series, 3 (Gordon and Breach Science, Philadelphia, PA, 1991).Google Scholar
Yang, G. and Liang, L., ‘Cartan–Eilenberg Gorenstein projective complexes’, J. Algebra Appl. 13 (2014), 1–17.Google Scholar