Article contents
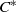 ${C}^{\ast } $-ALGEBRAS ASSOCIATED WITH LAMBDA-SYNCHRONIZING SUBSHIFTS AND FLOW EQUIVALENCE
${C}^{\ast } $-ALGEBRAS ASSOCIATED WITH LAMBDA-SYNCHRONIZING SUBSHIFTS AND FLOW EQUIVALENCE
Published online by Cambridge University Press: 07 August 2013
Abstract
The class of 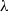 $\lambda $-synchronizing subshifts generalizes the class of irreducible sofic shifts. A
$\lambda $-synchronizing subshifts generalizes the class of irreducible sofic shifts. A 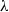 $\lambda $-synchronizing subshift can be presented by a certain
$\lambda $-synchronizing subshift can be presented by a certain 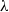 $\lambda $-graph system, called the
$\lambda $-graph system, called the 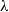 $\lambda $-synchronizing
$\lambda $-synchronizing 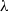 $\lambda $-graph system. The
$\lambda $-graph system. The 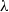 $\lambda $-synchronizing
$\lambda $-synchronizing  $\lambda $-graph system of a
$\lambda $-graph system of a 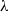 $\lambda $-synchronizing subshift can be regarded as an analogue of the Fischer cover of an irreducible sofic shift. We will study algebraic structure of the
$\lambda $-synchronizing subshift can be regarded as an analogue of the Fischer cover of an irreducible sofic shift. We will study algebraic structure of the 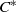 ${C}^{\ast } $-algebra associated with a
${C}^{\ast } $-algebra associated with a  $\lambda $-synchronizing
$\lambda $-synchronizing 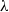 $\lambda $-graph system and prove that the stable isomorphism class of the
$\lambda $-graph system and prove that the stable isomorphism class of the 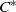 ${C}^{\ast } $-algebra with its Cartan subalgebra is invariant under flow equivalence of
${C}^{\ast } $-algebra with its Cartan subalgebra is invariant under flow equivalence of 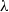 $\lambda $-synchronizing subshifts.
$\lambda $-synchronizing subshifts.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by

