Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T05:51:31.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain extensions and factorizations of α-complete homomorphisms in archimedean lattice-ordered groups

Part of: Ordered structures Topological linear spaces and related structures General theory of categories and functors

Published online by Cambridge University Press:  09 April 2009

Anthony W. Hager  and
Ann Kizanis
Anthony W. Hager
Affiliation:
Mathematics Department Wesleyan UniversityMiddletown, CT 06459, USA
Ann Kizanis
Affiliation:
Mathematics Department Western New England CollegeSpringfield, MA 01119, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As a consequence of general principles, we add to the array of ‘hulls’ in the category Arch (of archimedean ℓ-groups with ℓ-homomorphisms) and in its non-full subcategory W (whose objects have distinguished weak order unit, whose morphisms preserve the unit). The following discussion refers to either Arch or W. Let α be an infinite cardinal number or ∞, let Homα; denote the class of α-complete homomorphisms, and let R be a full epireflective subcategory with reflections denoted rG: G → rG. Then for each G, there is rαG ∈ Homα (G, R) such that for each ϕ ∈ Homα (G, R), there is unique 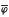with 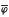. Moreover if every rG is an essential embedding, then, for every α and every G, rαG = rG, and every 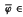Homα. If 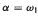and R consists of all epicomplete objects, then every 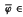Homw1. For α = ∞, and for any R, every 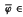Hom∞.

MSC classification

Secondary: 06F20: Ordered abelian groups, Riesz groups, ordered linear spaces 18A20: Epimorphisms, monomorphisms, special classes of morphisms, null morphisms 18A32: Factorization of morphisms, substructures, quotient structures, congruences, amalgams 46A40: Ordered topological linear spaces, vector lattices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 62 , Issue 2 , April 1997 , pp. 239 - 258
Copyright
Copyright © Australian Mathematical Society 1997

References

[AF]Anderson, M. and Feil, T., Lattice-ordered groups (Reidel, Dordrecht, 1988).Google Scholar
[BH1]Ball, R. N. and Hager, A. W., ‘Characterization of epimorphisms in archimedean ℓ-groups and vector lattices’, in: Lattice-ordered groups, advances and techniques (eds. Glass, A. and Holland, W. C.), (Kluwer, Dordrecht, 1989), Chapter 8.Google Scholar
[BH2]Ball, R. N. and Hager, A. W., ‘Epicomplete archimedean ℓ-groups’, Trans. Amer. Math. Soc. 32 (1990), 459–478.Google Scholar
[BH3]Ball, R. N. and Hager, A. W., ‘Epicompletion of archimedean ℓ-groups and vector lattices with weak unit’, J. Austral. Math. Soc. Series (A) 48 (1990), 25–56.CrossRefGoogle Scholar
[BH4]Ball, R. N. and Hager, A. W., ‘Algebraic extensions of an archimedean lattice-ordered group, I’, J. Pure and Appl. Algebra 85 (1993), 1–20.CrossRefGoogle Scholar
[BH5]Ball, R. N. and Hager, A. W., ‘Algebraic extensions of an archimedean lattice-ordered group, II’, to appear.Google Scholar
[BHM]Ball, R. N., Hager, A. W. and Macula, A. J., ‘An α-disconnected space has no proper monic preimage’, Topology Appl. 37 (1990), 141–151.CrossRefGoogle Scholar
[BKW]Bigard, A., Keimel, K. and Wolfenstein, S., Groups et anneaux réticulés, Lecture Notes in Math. 608 (Springer, Berlin, 1977).CrossRefGoogle Scholar
[C]Conrad, P. F., ‘The esssential closure of an archimedean lattice-ordered group’, Proc. London Math. Soc. 38 (1971), 151–160.Google Scholar
[DHH]Dashiell, F., Hager, A. W. and Henriksen, M., ‘Order-Cauchy completions of rings and vector lattices of continuous functions’, Canad. J. Math. 32 (1980), 657–685.Google Scholar
[F]Fremlin, D. H., ‘Inextensible Riesz spaces’, Math. Proc. Cambridge Philos. Soc. 77 (1975), 71–89.CrossRefGoogle Scholar
[GJ]Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand Co., Princeton, 1960); reprinted Graduate Texts in Math. 43, (Springer, Berlin, 1976).CrossRefGoogle Scholar
[H]Hager, A. W., ‘Algebraic closures of ℓ-groups of continuous functions’, in: Rings of continuous functions (ed. Aull, C.), Lecture Notes in Pure and Appl. Math. 95 (Dekker, New York, 1985) pp. 165–194.Google Scholar
[HM]Hager, A. W. and Martinez, J., ‘Maximum monoreflections’, Appl. Categ. Structures 2 (1994), 315–329.CrossRefGoogle Scholar
[HR]Hager, A. W. and Robertson, L. C., ‘On the embedding into a ring of an archimedean ℓ-group’, Canad. J. Math. 31 (1979), 1–8.CrossRefGoogle Scholar
[HS]Herrlich, H. and Strecker, G., Category theory (Allyn and Bacon, Boston, 1973).Google Scholar
[M]Macula, A. J., ‘α-Dedekind complete archimedean vector lattices versus α-quasi-F spaces’, Topology Appl. 44 (1992), 217–234.CrossRefGoogle Scholar
[S]Sikorski, R., Boolean algebras, 3rd edition, (Springer, Berlin, 1969).Google Scholar
[T]Tucker, C. T., ‘Concerning σ-homomorphisms of Riesz Spaces’, Pacific J. Math. 57 (1975), 585–590.Google Scholar
[TZ]Tzeng, Z., Extended-real-valued functions and the projective resolution of a compact Hausdorff space (PhD Thesis, Wesleyan University, 1970).Google Scholar
[V]Veksler, A. I., ‘P-sets in topological spaces’, Soviet Math. Dokl. 11 (1970) 953–956.Google Scholar