Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:22:04.867Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain homomorphisms of the lattice of varieties of completely simple semigroups

Part of: Semigroups

Published online by Cambridge University Press:  09 April 2009

Mario Petrich  and
Norman R. Reilly
Mario Petrich
Affiliation:
Simon Fraser UniversityBurnaby, British Columbia, Canada
Norman R. Reilly
Affiliation:
Simon Fraser UniversityBurnaby, British Columbia, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

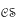Completely simple semigroups form a variety, , of algebras with the operations of multiplication and inversion. It is known that the mapping 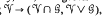, where 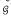is the variety of all groups, is an isomorphism of the lattice 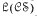of all subvarieties of 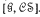onto a subdirect product of the lattice of subvarieties of and the interval . We consider embeddings of into certain direct products on the above pattern with rectangular bands, rectangular groups and central completely simple semigroups in place of groups.

MSC classification

Secondary: 20M05: Free semigroups, generators and relations, word problems 20M07: Varieties and pseudovarieties of semigroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 37 , Issue 3 , December 1984 , pp. 287 - 306
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Birkhoff, G., Lattice theory, 3rd ed., Amer. Math. Soc. Colloquium Publications, 25, Providence, R. I., 1967.Google Scholar
[2]Clifford, A. H., ‘The free completely regular semigroup’, J. Algebra 59 (1979), 434–451.CrossRefGoogle Scholar
[3]Hall, T. E. and Jones, P. R., ‘On the lattice of varieties of bands of groups’, Pacific J. Math. 91 (1980), 327–337.Google Scholar
[4]Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
[5]Jones, P. R., ‘Completely simple semigroups: free products, free semigroups and varieties’, Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 291–313.CrossRefGoogle Scholar
[6]Petrich, M., Introduction to semigroups (Merrill, Columbus, 1973).Google Scholar
[7]Petrich, M. and Reilly, N. R., ‘Varieties of groups and of completely simple semigroups’, Bull. Austral. Math. Soc. 23 (1981), 339–359.Google Scholar
[8]Petrich, M. and Reilly, N. R., ‘Near varieties of idempotent generated completely simple semigroups’, Algebra Universalis, to appear.Google Scholar
[9]Petrich, M. and Reilly, N. R., ‘All varieties of central completely simple semigroups’, Trans. Amer. Math. Soc. 280 (1983), 623–636.CrossRefGoogle Scholar
[10]Rasin, V. V., ‘Free completely simple semigroups’, Ural. Gos. Univ. Mat. Zap. 11 (1979), 140–151 (Russian).Google Scholar