Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T09:27:13.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of left Artinian algebras through pseudo path algebras

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  09 April 2009

Fang Li
Fang Li
Affiliation:
Department of MathematicsZhejiang UniversityHangzhou, Zhejiang 310027Chinafangli@zju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, using pseudo path algebras, we generalize Gabriel's Theorem on elementary algebras to left Artinian algebras over a field k when the quotient algebra can be lifted by a radical. Our particular interest is when the dimension of the quotient algebra determined by the nth Hochschild cohomology is less than 2 (for example, when k is finite or char k = 0). Using generalized path algebras, a generalization of Gabriel's Theorem is given for finite dimensional algebras with 2-nilpotent radicals which is splitting over its radical. As a tool, the so-called pseudo path algebra is introduced as a new generalization of path algebras, whose quotient by ken is a generalized path algebra (see Fact 2.6).

The main result is that

(i) for a left Artinian k–algebra A and r = r(A) the radical of A. if the quotient algebra A/r can be lifted then A ≅ PSEk (Δ, 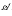, ρ) with Js ⊂ (ρ) ⊂ J for some s (Theorem 3.2);

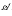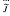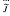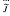(ii) If A is a finite dimensional k–algebra with 2-nilpotent radical and the quotient by radical can be lifted, then A ≅ k(Δ, , ρ) with 2 ⊂ (ρ) ⊂ 2 + ∩ ker 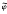(Theorem 4.2),

where Δ is the quiver of A and ρ is a set of relations.

For all the cases we discuss in this paper, we prove the uniqueness of such quivers Δ and the generalized path algebras/pseudo path algebras satisfying the isomorphisms when the ideals generated by the relations are admissible (see Theorem 3.5 and 4.4).

MSC classification

Secondary: 16G10: Representations of Artinian rings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 83 , Issue 3 , December 2007 , pp. 385 - 416
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Auslander, M.. Reiten, I. and Smalø, S. O., Representation Theory of Artin Algebras (CambridgeUniversity Press, 1995).CrossRefGoogle Scholar
[2]Coelho, F. U. and Liu, S. X., Generalized path algebras, volume 210 of Lecture Notes in Pure and Appl. Math. (Dekker, New York. 2000).Google Scholar
[3]Drozd, Y. A. and Kirichenko, V. V., Finite Dimensional Algebras (Springer-Verlag, Berlin, 1994).CrossRefGoogle Scholar
[4]Pierce, R. S., Associative Algebras (Springer-Verlag, New York. 1982).CrossRefGoogle Scholar
[5]Ringel, C. M.. Tame algebras and integral quadratic forms, volume 1099 of Lecture Notes in Math. (Springer-Verlag, 1984).CrossRefGoogle Scholar