Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T15:19:32.348Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZATIONS OF BMO AND LIPSCHITZ SPACES IN TERMS OF 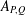$A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS

Part of: Harmonic analysis in several variables Special classes of linear operators

Published online by Cambridge University Press:  30 January 2019

DINGHUAI WANG ,
JIANG ZHOU  and
ZHIDONG TENG
DINGHUAI WANG*
Affiliation:
School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, China email Wangdh1990@126.com
JIANG ZHOU
Affiliation:
College of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, China email zhoujiang@xju.edu.cn
ZHIDONG TENG
Affiliation:
College of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, China email zhidong1960@163.com
*
✉Wangdh1990@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 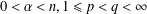$0<\unicode[STIX]{x1D6FC}<n,1\leq p<q<\infty$ with 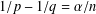$1/p-1/q=\unicode[STIX]{x1D6FC}/n$, 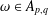$\unicode[STIX]{x1D714}\in A_{p,q}$, 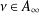$\unicode[STIX]{x1D708}\in A_{\infty }$ and let 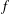$f$ be a locally integrable function. In this paper, it is proved that 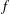$f$ is in bounded mean oscillation 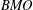$\mathit{BMO}$ space if and only if

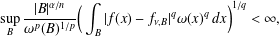$$\begin{eqnarray}\sup _{B}\frac{|B|^{\unicode[STIX]{x1D6FC}/n}}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty ,\end{eqnarray}$$
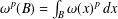where $\unicode[STIX]{x1D714}^{p}(B)=\int _{B}\unicode[STIX]{x1D714}(x)^{p}\,dx$ and 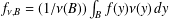$f_{\unicode[STIX]{x1D708},B}=(1/\unicode[STIX]{x1D708}(B))\int _{B}f(y)\unicode[STIX]{x1D708}(y)\,dy$. We also show that 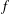$f$ belongs to Lipschitz space 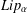$Lip_{\unicode[STIX]{x1D6FC}}$ if and only if
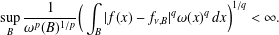$$\begin{eqnarray}\sup _{B}\frac{1}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty .\end{eqnarray}$$
 As applications, we characterize these spaces by the boundedness of commutators of some operators on weighted Lebesgue spaces.

Keywords

Ap, q weightsBMO spacecharacterizecommutatorsLipschitz spaces

MSC classification

Primary: 47B47: Commutators, derivations, elementary operators, etc.
Secondary: 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 381 - 391
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bloom, S., ‘A commutator theorem and weighted BMO’, Trans. Amer. Math. Soc. 292 (1985), 103–122.Google Scholar
Chanillo, S., ‘A note on commutators’, Indiana Univ. Math. J. 31 (1982), 7–16.Google Scholar
Coifman, R., Rochberg, R. and Weiss, G., ‘Factorization theorems for Hardy spaces in several variables’, Ann. of Math. (2) 103 (1976), 611–635.Google Scholar
Cruz-Uribe, D. and Fiorenza, A., ‘Endpoint estimates and weighted norm inequalities for commutators of fractional integrals’, Publ. Math. 47 (2003), 103–131.Google Scholar
Devore, R. A. and Sharpley, R. C., Maximal Functions Measuring Smoothness, Memoirs of the American Mathematical Society, 47 (American Mathematical Society, 1984).Google Scholar
Ding, Y., ‘A characterization of BMO via commutators for some operators’, Northeast. Math. J. 13 (1997), 422–432.Google Scholar
Grafakos, L., Classical and Modern Fourier Analysis (Springer, New York, 2004).Google Scholar
Hart, J. and Torres, R. H., ‘John–Nirenberg inequalities and weight invariant BMO spaces’, J. Geom. Anal. 1 (2018), 1–41.Google Scholar
Ho, K.-P., ‘Characterization of BMO by a p weights and p-convexity’, Hiroshima Math. J. 41 (2011), 153–165.Google Scholar
Janson, S., Taibleson, M. and Weiss, G., ‘Elementary characterization of the Morrey–Campanato spaces’, Lect. Notes Math. 992 (1983), 101–114.Google Scholar
John, F. and Nirenberg, L., ‘On functions of bounded mean oscillation’, Comm. Pure Appl. Math. 2 (1961), 415–426.Google Scholar
Muckenhoupt, B., ‘Weighted norm inequalities for the Hardy maximal function’, Trans. Amer. Math. Soc. 165 (1972), 207–226.Google Scholar
Muckenhoupt, B. and Wheeden, R., ‘Weighted bounded mean oscillation and the Hilbert transform’, Studia Math. 54 (1975), 221–237.Google Scholar
Muckenhoupt, B. and Wheeden, R., ‘Weighted norm inequalities for fractional integrals’, Trans. Amer. Math. Soc. 192 (1974), 261–274.Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton, NJ, 1993).Google Scholar
Wang, D. H., Zhou, J. and Teng, Z. D., ‘A note on Campanato spaces and their applications’, Math. Notes 103 (2018), 483–489.Google Scholar