Published online by Cambridge University Press: 21 October 2015
This paper is devoted to dualization of paracompactness to the coarse category via the concept of 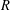 $R$-disjointness. Property A of Yu can be seen as a coarse variant of amenability via partitions of unity and leads to a dualization of paracompactness via partitions of unity. On the other hand, finite decomposition complexity of Guentner, Tessera, and Yu and straight finite decomposition complexity of Dranishnikov and Zarichnyi employ
$R$-disjointness. Property A of Yu can be seen as a coarse variant of amenability via partitions of unity and leads to a dualization of paracompactness via partitions of unity. On the other hand, finite decomposition complexity of Guentner, Tessera, and Yu and straight finite decomposition complexity of Dranishnikov and Zarichnyi employ 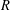 $R$-disjointness as the main concept. We generalize both concepts to that of countable asymptotic dimension and our main result shows that it is a subclass of spaces with Property A. In addition, it gives a necessary and sufficient condition for spaces of countable asymptotic dimension to be of finite asymptotic dimension.
$R$-disjointness as the main concept. We generalize both concepts to that of countable asymptotic dimension and our main result shows that it is a subclass of spaces with Property A. In addition, it gives a necessary and sufficient condition for spaces of countable asymptotic dimension to be of finite asymptotic dimension.