Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T03:59:05.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Commutative subsemigroups of the composition semigroup of formal power series over an integral domain

Published online by Cambridge University Press:  09 April 2009

Hermann Kautschitsch
Hermann Kautschitsch
Affiliation:
Universität für BildungswissenschaftenA—9010 Klagenfurt, Universitätsstrasse 67, Austria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with identity. R[[x]] denotes the ring of formal power series, in which we consider the composition ○, defined by f(x)○g(x)=f(g(x)). This operation is well defined in the subring R+[[x]] of formal power series of positive order. The algebra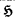= 〈R+[[x]], ○〉 is learly a semigroup, which is not commutative for ∣R∣>1. In this paper we consider all those commutative subsemigroups of 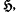, which consist of power series of all positive orders, which are called ‘permutable chains’.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 27 , Issue 3 , May 1979 , pp. 313 - 318
Copyright
Copyright © Australian Mathematical Society 1979

References

Baker, J. N. (1961–1962), ‘Permutable power series and regular iteration’, J. Australian Math. Soc. 2, 265–294.CrossRefGoogle Scholar
Gradstkeyn, J. S. and Ryzhik, J. M. (1965), Table of integrals, series and products (Academic Press, New York).Google Scholar
Kautschitsch, H. (1970), ‘Kommutative Teilhalbgruppen der Kompositionshalbgruppe von Polynomen und formalen Potenzreihen’, Monatsh. f. Math. 74, 421–436.CrossRefGoogle Scholar
Lausch, H. and Nöbauer, W. (1973), Algebra of polynomials (North-Holland Mathematical Library, Vol. 5, Amsterdam and London).Google Scholar