Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T19:31:25.607Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTINUOUS ASSOCIATION SCHEMES AND HYPERGROUPS

Part of: Abstract harmonic analysis Algebraic combinatorics Other generalizations of groups

Published online by Cambridge University Press:  27 July 2018

MICHAEL VOIT
MICHAEL VOIT*
Affiliation:
Fakultät Mathematik, Technische Universität Dortmund, Vogelpothsweg 87, D-44221 Dortmund, Germany email michael.voit@math.tu-dortmund.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Classical finite association schemes lead to finite-dimensional algebras which are generated by finitely many stochastic matrices. Moreover, there exist associated finite hypergroups. The notion of classical discrete association schemes can be easily extended to the possibly infinite case. Moreover, this notion can be relaxed slightly by using suitably deformed families of stochastic matrices by skipping the integrality conditions. This leads to a larger class of examples which are again associated with discrete hypergroups. In this paper we propose a topological generalization of association schemes by using a locally compact basis space 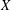$X$ and a family of Markov-kernels on 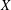$X$ indexed by some locally compact space 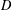$D$ where the supports of the associated probability measures satisfy some partition property. These objects, called continuous association schemes, will be related to hypergroup structures on 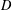$D$. We study some basic results for this notion and present several classes of examples. It turns out that, for a given commutative hypergroup, the existence of a related continuous association scheme implies that the hypergroup has many features of a double coset hypergroup. We, in particular, show that commutative hypergroups, which are associated with commutative continuous association schemes, carry dual positive product formulas for the characters. On the other hand, we prove some rigidity results in particular in the compact case which say that for given spaces 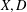$X,D$ there are only a few continuous association schemes.

Keywords

association schemesGelfand pairshypergroupsspherical functionspositive definite functionspositive product formulasrigidity resultsrandom walks on association schemes

MSC classification

Primary: 43A62: Hypergroups
Secondary: 05E30: Association schemes, strongly regular graphs 33C67: Hypergeometric functions associated with root systems 20N20: Hypergroups 43A90: Spherical functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 3 , June 2019 , pp. 361 - 426
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Abramenko, P., Parkinson, J. and van Maldeghem, H., ‘Distance regularity in buildings and structure constants in Hecke algebras’, J. Algebra 481 (2017), 158–187.Google Scholar
Askey, R., Orthogonal Polynomials and Special Functions, Regional Conference Series in Applied Mathematics, 21 (SIAM, Philadelphia, PA, 1975).Google Scholar
Askey, R. and Wilson, J. A., ‘Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials’, Mem. Amer. Math. Soc. 54(319) (1985), 55 pages.Google Scholar
Bailey, R. A., Association Schemes: Designed Experiments, Algebra and Combinatorics, Cambridge Studies in Mathematics, 84 (Cambridge University Press, Cambridge, MA, 2004).Google Scholar
Bannai, E. and Ito, T., Algebraic Combinatorics I: Association Schemes (Benjamin/Cummings, Menlo Park, CA, 1984).Google Scholar
Berg, C. and Forst, G., Potential Theory on Locally Compact Abelian Groups (Springer, Berlin, 1974).Google Scholar
Bingham, N., ‘Random walks on spheres’, Z. Wahrscheinlichkeitsth. verw. Geb. 22 (1972), 169–192.Google Scholar
Bloom, W. R. and Heyer, H., Harmonic Analysis of Probability Measures on Hypergroups (de Gruyter-Verlag Berlin, New York, 1995).Google Scholar
Bougerol, P., ‘The Matsumoto and Yor process and infinite dimensional hyperbolic space’, in: Memoriam Marc Yor. Sminaire de Probabilits XLVII, Lecture Notes in Mathematics, 2137 (eds. Donati-Martin, C. et al. ) (Springer, Berlin, 2015).Google Scholar
Brouwer, A. E., Cohen, A. M. and Neumaier, A., Distance-regular Graphs (Springer, Berlin, 1989).Google Scholar
Chapovski, Y., ‘Existence of an invariant measure on a locally compact hypergroup’, Preprint, 2012, arXiv:1212.6571.Google Scholar
van Dam, E. R., Koolen, J. H. and Tanaka, H., ‘Distance-regular graphs’, in: Electron. J. Combin. DS22, Dynamic Survey (2016), 156.Google Scholar
van Dijk, G., Introduction to Harmonic Analysis and Generalized Gelfand Pairs (de Gruyter, Berlin, 2009).Google Scholar
Dugundji, J., Topology (Allyn and Bacon, Boston, MA, 1966).Google Scholar
Dunkl, C. F., ‘The measure algebra of a locally compact hypergroup’, Trans. Amer. Math. Soc. 179 (1973), 331–348.Google Scholar
Faraut, J., ‘Analyse harmonique sur les pairs de Gelfand et les espaces hyperboliques’, in: Analyse Harmonique (eds. Clerc, J.-L. et al. ) (C.I.M.P.A., Nice, 1982), Ch. IV.Google Scholar
Flensted-Jensen, M. and Koornwinder, T., ‘Jacobi functions: The addition formula and the positivity of the dual convolution structure’, Ark. Mat. 17 (1979), 139–151.Google Scholar
Flensted-Jensen, M. and Koornwinder, T., ‘Positive definite spherical functions on a non-compact rank one symmetric space’, in: Analyse harmonique sur les groupes de Lie II, Lecture Notes in Mathematics, 739 (eds. Eymard, P. et al. ) (Springer, Berlin, 1979), 249–282.Google Scholar
Helgason, S., Groups and Geometric Analysis (American Mathematical Society, Providence, RI, 2000).Google Scholar
Heyer, H., Katayama, Y., Kawakami, S. and Kawasaki, K., ‘Extensions of finite commutative hypergroups’, Sci. Math. Jpn. 65 (2007), 373–385.Google Scholar
Heyer, H., Kawakami, S. and Yamanaka, S., ‘Characters of induced representations of a compact hypergroup’, Monatsh. Math. 179 (2016), 421–440.Google Scholar
Jewett, R. I., ‘Spaces with an abstract convolution of measures’, Adv. Math. 18 (1975), 1–101.Google Scholar
Kaimanovich, V. A. and Woess, W., ‘Construction of discrete, non-unimodular hypergroups’, in: Probability Measures on Groups and Related Structures, XI (ed. Heyer, H.) (World Scientific Publishing, Singapore, 1995), 196–209.Google Scholar
Kallenberg, O., Foundations of Modern Probability (Springer, New York, 1997).Google Scholar
Kashiwara, M., Kowata, A., Minemura, K., Okamoto, K., Oshima, T. and Tanaka, M., ‘Eigenfunctions of invariant differential operators on a symmetric space’, Ann. of Math. (2) 107 (1978), 1–39.Google Scholar
Kingman, J. F. C., ‘Random walks with spherical symmetry’, Acta Math. 109 (1963), 11–53.Google Scholar
Koornwinder, T., ‘Jacobi functions and analysis on noncompact semisimple Lie groups’, in: Special Functions: Group Theoretical Aspects and Applications (eds. Askey, R. et al. ) (D Reidel, Dordrecht–Boston–Lancaster, 1984).Google Scholar
Koornwinder, T. and Schwartz, A. L., ‘Product formulas and associated hypergroups for orthogonal polynomials on the simplex and on a parabolic biangle’, Constr. Approx. 13 (1997), 537–567.Google Scholar
Lasser, R., ‘Orthogonal polynomials and hypergroups’, Rend. Mat. 3(2) (1983), 185–209.Google Scholar
Letac, G., ‘Dual random walks and special functions on homogeneous trees’, in: Random walks and stochastic processes on Lie groups, Institut Élie Cartan, 7 (Univ. Nancy, 1983), 97–142.Google Scholar
Macpherson, H. D., ‘Infinite distance transitive graphs of finite valency’, Combinatorica 2 (1982), 63–69.Google Scholar
Rösler, M., ‘Bessel convolutions on matrix cones’, Compos. Math. 143 (2007), 749–779.Google Scholar
Rudin, W., Functional Analysis (McGraw-Hill, New York, 1973).Google Scholar
Sunder, V. S. and Wildberger, N. J., ‘Fusion rule algebras and walks on graphs’, in: Proc. Fifth Ramanujan Symposium on Harmonic Analysis (ed. Parthasarathy, K. R.) (Ramanujan Institute, 1999), 53–80.Google Scholar
Titchmarsh, E. C., The Theory of Functions (Oxford University Press, London, 1939).Google Scholar
Voit, M., ‘Positive characters on commutative hypergroups and some applications’, Math. Z. 198 (1988), 405–421.Google Scholar
Voit, M., ‘Central limit theorems for random walks on ℕ0 that are associated with orthogonal polynomials’, J. Multivariate Anal. 34 (1990), 290–322.Google Scholar
Voit, M., ‘On the dual space of a commutative hypergroup’, Arch. Math. 56 (1991), 380–385.Google Scholar
Voit, M., ‘On the Fourier transformation of positive, positive definite measures on commutative hypergroups and dual convolution structures’, Man. Math. 72 (1991), 141–153.Google Scholar
Voit, M., ‘Projective and inductive limits of hypergroups’, Proc. Lond. Math. Soc. (3) 67 (1993), 617–648.Google Scholar
Voit, M., ‘Substitution of open subhypergroups’, Hokkaido Math. J. 233 (1994), 143–183.Google Scholar
Voit, M., ‘A product formula for orthogonal polynomials associated with infinite distance-transitive graphs’, J. Approx. Theory 120 (2003), 337–354.Google Scholar
Voit, M., ‘Generalized commutative association schemes, hypergroups, and positive product formulas’, Commun. Stoch. Anal. 10(4) (2016), 561–585.Google Scholar
Voit, M., ‘Homogeneous trees and generalized association schemes’. Preprint, 2017.Google Scholar
Wildberger, N. J., ‘Finite commutative hypergroups and applications from group theory to conformal field theory’, Contemp. Math. 183 (1995), 413–434.Google Scholar
Wildberger, N. J., ‘Lagrange’s theorem and integrality for finite commutative hypergroups with applications to strongly regular graphs’, J. Algebra 182 (1996), 1–37.Google Scholar
Zeuner, H. M., ‘Properties of the cosh hypergroup’, in: Probability measures on groups IX, Lecture Notes in Mathematics, 1379 (ed. Heyer, H.) (Springer, Berlin–New York, 1988), 425–434.Google Scholar
Zieschang, P.-H., Theory of Association Schemes (Springer, Berlin, 2005).Google Scholar