Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:38:39.430Z Has data issue: false hasContentIssue false
  • English
  • Français

DETERMINING ASCHBACHER CLASSES USING CHARACTERS

Part of: Representation theory of groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  11 November 2014

SEBASTIAN JAMBOR
SEBASTIAN JAMBOR*
Affiliation:
Department of Mathematics, The University of Auckland, Private Bag 92019, Auckland, New Zealand email s.jambor@auckland.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 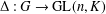${\rm\Delta}:G\rightarrow \text{GL}(n,K)$ be an absolutely irreducible representation of an arbitrary group 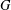$G$ over an arbitrary field 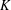$K$; let 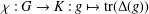${\it\chi}:G\rightarrow K:g\mapsto \text{tr}({\rm\Delta}(g))$ be its character. In this paper, we assume knowledge of 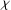${\it\chi}$ only, and study which properties of 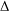${\rm\Delta}$ can be inferred. We prove criteria to decide whether ${\rm\Delta}$ preserves a form, is realizable over a subfield, or acts imprimitively on 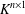$K^{n\times 1}$. If 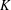$K$ is finite, we can decide whether the image of 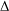${\rm\Delta}$ belongs to certain Aschbacher classes.

Keywords

representations of groupscharacter theoryAschbacher classification

MSC classification

Primary: 20C99: None of the above, but in this section
Secondary: 20G15: Linear algebraic groups over arbitrary fields
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 355 - 363
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76(3) (1984), 469–514.CrossRefGoogle Scholar
Carayol, H., ‘Formes modulaires et représentations galoisiennes à valeurs dans un anneau local complet’, in: p-adic Monodromy and the Birch and Swinnerton-Dyer Conjecture, Boston, MA, 1991, Contemporary Mathematics, 165 (American Mathematical Society, Providence, RI, 1994), 213–237.Google Scholar
Carlson, J. F., Neunhöffer, M. and Roney-Dougal, C. M., ‘A polynomial-time reduction algorithm for groups of semilinear or subfield class’, J. Algebra 322(3) (2009), 613–637.CrossRefGoogle Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups, Graduate Texts in Mathematics, 163 (Springer, New York, 1996).CrossRefGoogle Scholar
Glasby, S. P. and Howlett, R. B., ‘Writing representations over minimal fields’, Comm. Algebra 25(6) (1997), 1703–1711.CrossRefGoogle Scholar
Glasby, S. P., Leedham-Green, C. R. and O’Brien, E. A., ‘Writing projective representations over subfields’, J. Algebra 295(1) (2006), 51–61.CrossRefGoogle Scholar
Holt, D. F., Leedham-Green, C. R., O’Brien, E. A. and Rees, S., ‘Testing matrix groups for primitivity’, J. Algebra 184(3) (1996), 795–817.CrossRefGoogle Scholar
Jacobson, N., Basic Algebra. II, 2nd edn (W. H. Freeman, New York, 1989).Google Scholar
Jambor, S., ‘An $\text{L}_{3}$ – $\text{U}_{3}$ -quotient algorithm for finitely presented groups’, PhD Thesis, RWTH Aachen University, 2012.Google Scholar
Jambor, S., ‘An L2-quotient algorithm for finitely presented groups on arbitrarily many generators’, J. Algebra, to appear.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘On the subgroup structure of classical groups’, Invent. Math. 134(2) (1998), 427–453.CrossRefGoogle Scholar
Lux, K. and Pahlings, H., Representations of Groups: A Computational Approach, Cambridge Studies in Advanced Mathematics, 124 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Nakamoto, K., ‘Representation varieties and character varieties’, Publ. Res. Inst. Math. Sci. 36(2) (2000), 159–189.CrossRefGoogle Scholar
Niemeyer, A. C. and Praeger, C. E., ‘A recognition algorithm for classical groups over finite fields’, Proc. Lond. Math. Soc. (3) 77(1) (1998), 117–169.CrossRefGoogle Scholar
Plesken, W. and Fabiańska, A., ‘An L 2-quotient algorithm for finitely presented groups’, J. Algebra 322(3) (2009), 914–935.CrossRefGoogle Scholar