Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Uchida, Yoshihisa
1999.
Algebraic Independence of the Power Series Defined by Blocks of Digits.
Journal of Number Theory,
Vol. 78,
Issue. 1,
p.
107.
Allouche, Jean-Paul
and
Shallit, Jeffrey
2003.
The ring of k-regular sequences, II.
Theoretical Computer Science,
Vol. 307,
Issue. 1,
p.
3.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
329.
Cusick, Thomas W.
and
Ciungu, Lavinia Corina
2011.
Sum of digits sequences modulo m.
Theoretical Computer Science,
Vol. 412,
Issue. 35,
p.
4738.

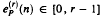 counts the number of occurrences (mod
counts the number of occurrences (mod 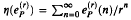 is transcendental except when
is transcendental except when 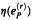 has infinite dimension over Q, where
has infinite dimension over Q, where 