Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tong, Jingcheng
1996.
Robinson's Theorem on Asymmetric Diophantine Approximation.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 1,
TONG, JINGCHENG
2004.
SYMMETRIC AND ASYMMETRIC DIOPHANTINE APPROXIMATION.
Chinese Annals of Mathematics,
Vol. 25,
Issue. 01,
p.
139.
Kraaikamp, Cornelis
and
Smeets, Ionica
2011.
Sharp bounds for symmetric and asymmetric diophantine approximation.
Chinese Annals of Mathematics, Series B,
Vol. 32,
Issue. 2,
p.
303.

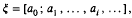
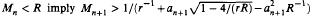 which generalizes a previous result of the author.
which generalizes a previous result of the author.