Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shvedenko, S. V.
1987.
Hardy classes and related spaces of analytic functions in the unit circle, polydisc, and ball.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 6,
p.
3011.
Chow, Kwang -Nan
and
Protas, David
1991.
Boundary conditions for a finite Dirichlet integral in the upper half plane.
Archiv der Mathematik,
Vol. 57,
Issue. 5,
p.
479.


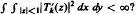 We shall show, among other results, that the answer is in the positive if
We shall show, among other results, that the answer is in the positive if 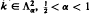 , with ess inf
, with ess inf 