Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gulliver, T.Aaron
and
Harada, Masaaki
2001.
Orthogonal Frames in the Leech Lattice and a Type II Code over Z22.
Journal of Combinatorial Theory, Series A,
Vol. 95,
Issue. 1,
p.
185.
Georgiou, Stelios
Harada, Masaaki
and
Koukouvinos, Christos
2002.
Orthogonal Designs and Type II Codes over ℤ2k
.
Designs, Codes and Cryptography,
Vol. 25,
Issue. 2,
p.
163.
Harada, Masaaki
and
Kitazume, Masaaki
2002.
Z6-Code Constructions of the Leech Lattice and the Niemeier Lattices.
European Journal of Combinatorics,
Vol. 23,
Issue. 5,
p.
573.
Shimakura, Hiroki
2002.
Decompositions of the Moonshine Module with Respect to subVOAs Associated to Codes over Z2k.
Journal of Algebra,
Vol. 251,
Issue. 1,
p.
308.
Harada, Masaaki
2009.
On the existence of frames of the Niemeier lattices and self-dual codes over Fp.
Journal of Algebra,
Vol. 321,
Issue. 8,
p.
2345.
Harada, Masaaki
and
Miezaki, Tsuyoshi
2011.
An upper bound on the minimum weight of Type II Z2k-codes.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 1,
p.
190.
Munemasa, Akihiro
and
Tamura, Hiroki
2012.
The codes and the lattices of Hadamard matrices.
European Journal of Combinatorics,
Vol. 33,
Issue. 4,
p.
519.
Miezaki, Tsuyoshi
2012.
Frames in the odd Leech lattice.
Journal of Number Theory,
Vol. 132,
Issue. 12,
p.
2773.
Alves, Carina
and
Costa, Sueli I.R.
2013.
Commutative group codes inR4,R6,R8andR16—Approaching the bound.
Discrete Mathematics,
Vol. 313,
Issue. 16,
p.
1677.
Harada, Masaaki
and
Miezaki, Tsuyoshi
2013.
On the existence of extremal Type II ℤ_{2𝕜}-codes.
Mathematics of Computation,
Vol. 83,
Issue. 287,
p.
1427.
Harada, Masaaki
2015.
Extremal Type I <inline-formula> <tex-math notation="LaTeX">$ \mathbb {Z}_{k}$ </tex-math></inline-formula>-Codes and <inline-formula> <tex-math notation="LaTeX">$k$ </tex-math></inline-formula>-Frames of Odd Unimodular Lattices.
IEEE Transactions on Information Theory,
Vol. 61,
Issue. 1,
p.
72.
Harada, Masaaki
2023.
Construction of extremal Type II Z2k-codes.
Finite Fields and Their Applications,
Vol. 87,
Issue. ,
p.
102154.

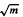 in the Leech lattice. We give such a construction by means of double circulant codes whenever
in the Leech lattice. We give such a construction by means of double circulant codes whenever 