Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T10:38:54.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding semirings in semirings with multiplicative unit

Published online by Cambridge University Press:  09 April 2009

K. R. Pearson
K. R. Pearson
Affiliation:
University of AdelaideSouth Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A topological semiring is a system (S, +, ·) where (S, +) and (S, ·) are topological semigroups and · distributes across + as in a ring; that is, for all x, y, z in S, 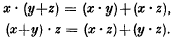The operations + and · are called addition and multiplication respectively.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 2 , May 1968 , pp. 183 - 191
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Bourbaki, N., Topologie générale (Actualités scientifiques et industrielles no. 1142, 1961).Google Scholar
[2]Hewitt, E., ‘Compact monothetic semigroups’, Duke Math. J. 23 (1956), 447–457.CrossRefGoogle Scholar
[3]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, Vol. 1 (Springer-Verlag, Berlin, 1963).Google Scholar
[4]Kurosh, A. G.Lectures on general algebra (Chelsea, New York, 1963).Google Scholar
[5]Miranda, A. B. Paalman-de, Topological semigroups (Mathematisch Centrum, Amsterdam, 1964).Google Scholar
[6]Selden, J., Theorems on topological semigroups and semirings (Doctoral Dissertation, University of Georgia, 1963).Google Scholar
[7]Selden, J., ‘A note on compact semirings’ Proc. Amer. Math. Soc. 17 (1966), 882–886.Google Scholar
[8]Wallace, A. D., ‘The structure of topological semigroups’, Bull. Amer. Math. Soc. 61 (1955), 95–112.CrossRefGoogle Scholar
[9]Zassenhaus, H., The theory of groups (2nd ed., Chelsea, New York, 1958).Google Scholar